摘要:為降低流體黏度對渦輪流量計測量精度的影響,將渦輪流量計儀表系數線性度誤差最小值作為目標函數,在運用計算流體力學(CFD)仿真的基礎上,先通過Plackett-Burman設計篩選結構參數,并根據幾何結構對目標函數的影響將其劃分為兩個等級,即顯著影響因素和次顯著影響因素;再通過Box-Behnken設計及響應面法對顯著影響因素進行優化設計,分析結構參數間的交互作用,得到參數的設計點;最后在響應面分析基礎上通過正交試驗對次顯著影響因素進行優化設計,得到最優參數組合。對參數組合的渦輪流量計進行試驗研究,試驗結果與CFD計算值吻合,儀表系數線性度誤差由1.71%下降至1.59%,表明優化后的渦輪流量計測量精度得到了顯著提高,基于響應面法和正交試驗的優化方法可以用于渦輪流量計的結構設計。
引言
渦輪流量計具有精度高、重復性好、結構簡單、測量范圍廣、體積小、質量輕、壓力損失小、維修方便等優點,但存在性能會隨被測流體黏度增大而變差的問題。目前,國內的渦輪流量計在出廠時,其性能一般都是用水或黏度比較低的柴油進行鑒定,但很多使用者卻用渦輪流量計來測量液壓油、潤滑油等中黏度甚至高黏度液體的流量,導致出現很大的測量誤差。因此,提高渦輪流量計在測量黏性介質時的精度具有非常重要的現實意義。
目前關于黏性介質對渦輪流量計影響的研究主要集中在分析流量計內部幾何結構和流體介質對其性能的影響以及儀表系數的修正方法等方面,而根據流體性能對流量計進行結構優化的研究較少,在結構優化時考慮到內部幾何參數間交互作用的則更少。由于渦輪流量計幾何參數較多,作用的機理各不相同,各個參數之間存在交互作用,因此有必要研究各個參數間的相互關系,確定最優參數組合。以DN40渦輪流量計為例,從優化幾何結構出發,探究幾何參數對渦輪流量計性能的影響,分析顯著影響因素之間的交互作用,并在計算流體力學(CFD)仿真的基礎上通過響應面法和正交試驗對結構進行優化設計。
1模型與仿真
1.1模型的建立
選擇LWGY系列DN40渦輪流量計,其主要參數為:葉輪葉片數N1=6,葉片頂端半徑Rt=9.5mm,葉輪輪轂半徑Ro=10mm,葉輪輪轂長度Lh=8mm,葉輪導程L=88.5mm,導流體葉片數N2=4,前導流體輪轂長度H1=54mm,后導流體輪轂長度H2=38mm。按照上述幾何參數建立三維模型,如圖1所示。為了使流體接近充分發展狀態從而形成穩定的流速分布,在渦輪流量計前后分別加裝10D和5D長直管段[10]。
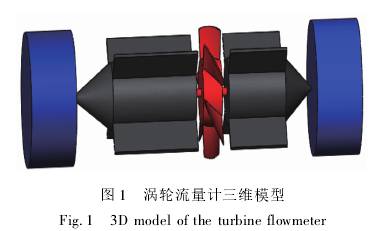
1.2網格劃分
將三維模型導入網格劃分軟件ICEM中,考慮圖1渦輪流量計三維模型Fig.13Dmodeloftheturbineflowmeter到流量計葉輪部分和導流件部分結構復雜,而且是仿真計算的關鍵部件,因此在ICEM中均采用非結構化的四面體網格對葉輪流域和導流件流域進行劃分;而前、后直管段流域結構相對簡單但尺寸較大,采用四面體網格劃分會使網格數量大大增加,為了減少仿真時間,采用結構化的六面體網格對該流域進行劃分,劃分后的網格數為1474621個,其Quali-ty最小值為0.36。通過增加整體網格數進行網格無關性檢驗,網格尺度符合計算要求。
1.3邊界條件定義
邊界條件如下:
(1)仿真介質采用實際狀況下的原油,其運動黏度為2.64×10-5m2/s,密度為887kg/m3,流量范圍2~20m3/h;
(2)入口采用速度入口,選取2m3/h、4m3/h、8m3/h、14m3/h、20m3/h這5個體積流量下的入口速度;出口采用壓力出口,設置為1個標準大氣壓;
(3)管壁,上、下導流體和葉輪表面均采用無滑移壁面邊界條件;
(4)渦輪流量計葉輪部分流域設置為旋轉流域,前后導流件部分設置為固定流域,旋轉流域與固定流域之間采用交界面進行連接。
1.4湍流模型的選擇
由于渦輪流量計葉輪在流體中處于高速旋轉狀態,其表面曲率變化非常大,而雷諾應力模型(RSM)考慮到了流體旋轉或流線彎曲所帶來的應力張量的急劇變化,可以更好地模擬渦輪流量計在復雜流場狀況下的運行規律,因此選用RSM湍流模型[11]。
1.5仿真儀表系數和線性度誤差的計算
儀表系數為渦輪感應放大器產生的脈沖數與流過傳感器流體體積的比值[12]。在計算仿真儀表系數之前需要計算流量計葉輪在該流量下的穩定轉速θ。通過監測發現,當葉輪驅動力矩與阻力矩的差值小于10-8時,可認為葉輪所受力矩達到平衡,則此時的葉輪轉速即為穩定轉速。葉輪穩定轉速確定后,根據葉片個數、入口流速與管道截面積可以得到此時的渦輪流量計仿真儀表系數,其計算公式為
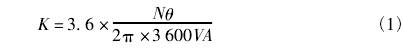
式中,K為渦輪流量計仿真儀表系數,L-1;N為葉輪葉片個數;?為葉輪穩定轉速,rad/s;V為入口流速,m/s;A為前直管段入口截面積,m2
儀表系數線性度誤差可以反映渦輪流量計的測量精度,儀表系數線性度誤差越小,則流量計的測量精度越高,反之則測量精度越低。
通過式(1)計算出2m3/h、4m3/h、8m3/h、14m3/h、20m3/h這5個點的仿真儀表系數后,便可以得到渦輪流量計儀表系數線性度誤差8,其計算公式為

式中Kmin,i為流量計在5個流量點處得到的儀表系數最大值;Kmin,i,為流量計在5個流量點處得到的儀表系數最小值。
2Plackett-Burman設計
根據.Plackett-Burman(PB)試驗設計,選取8個試驗因素(葉輪頂端半徑、葉輪葉片數、葉輪輪轂半徑、葉輪輪轂長度、葉輪導程、前導流件長度、后導流件長度、導流體葉片數)和3個空白因素,每個因素設高、低兩個水平,以儀表系數線性度誤差為響應值,共計12個試驗,試驗設計因素及水平見表1。
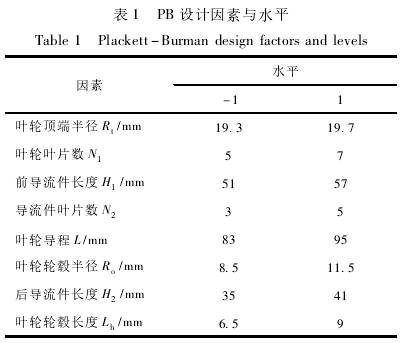
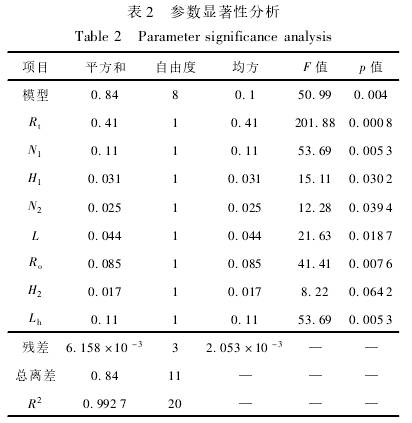
對表1試驗中各因素進行顯著性分析,分析結果如表2所示,模型顯著差異水平p=0.004,說明.回歸方程關系顯著;決定系數R2=0.9927,說明回歸有效,試驗結果可靠。由表2還可以看出8個因素均對流量計線性度誤差影響顯著,其中葉輪葉片數N1、葉輪頂端半徑R1、葉片輪轂半徑R.。、葉輪輪轂長度Lh這4個為顯著影響參數,在后文中運用響應面法進行優化;而葉輪導程L、前導流件長度H1、后導流件長度H2、導流體葉片數N2這4個為次顯著影響參數,在后文中運用正交試驗進行優化。
3結構參數優化.
3.1顯著影響參數的響應面法優化
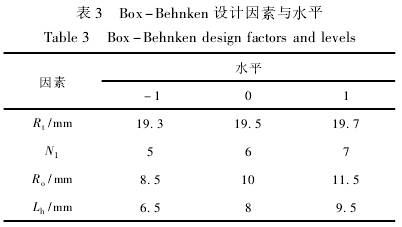
采用Box-Behnken中心組合設計方法,以葉輪頂端半徑Rt、葉片數N1、葉片輪轂半徑R.。、葉輪輪轂長度Lh這4個顯著影響因素為自變量,儀表系數線性度誤差為響應值,其余結構參數保持不變,設計四因素三水平29個試驗點的響應面優化試驗。因素與水平見表3,試驗設計見表4。
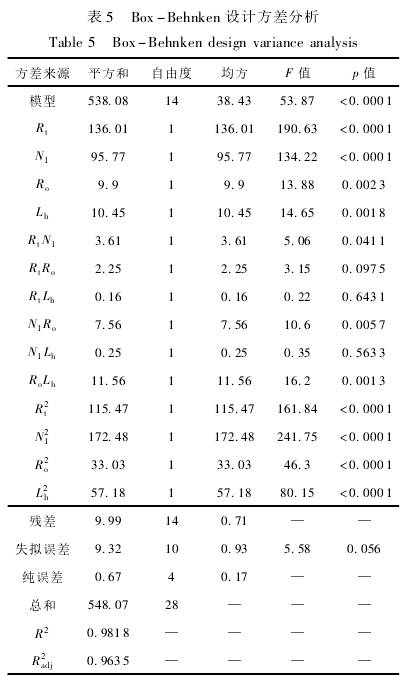
對模型進行方差分析得到的響應面分析結果如
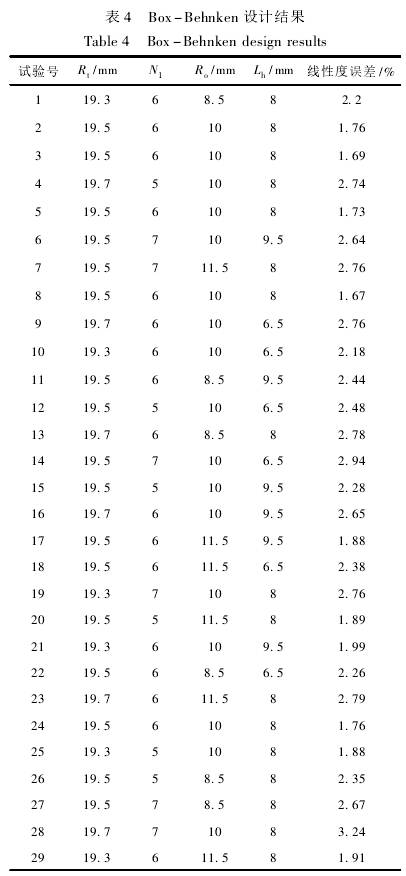
表5所示,p<0.0001<0.05,表明該模型是顯著的,具有統計學意義。由表5數據可得,自變量R、N、R。、Lh均顯著(p<0.05),按照對響應值的影響程度排序為葉輪頂端半徑R1>葉輪葉片數N1>葉輪輪轂長度Lh>葉輪輪轂半徑R。失擬項P=0.056>0.05,此值不顯著,說明在試驗范圍內預測值和實測值的擬合度較高,能夠選擇該回歸方程對試驗結果進行相關分析,線性度誤差R的回歸方程為
R=17.22+3.37Rt+2.82N1-0.91R。-0.93Lh-0.95RtN1+0.75R1R。+0.2R1Lh+1.38N1R。-0.25N1Lh-1.70R。Lh+4.22R21+5.16N21+2.26R2。+2.97Lh2
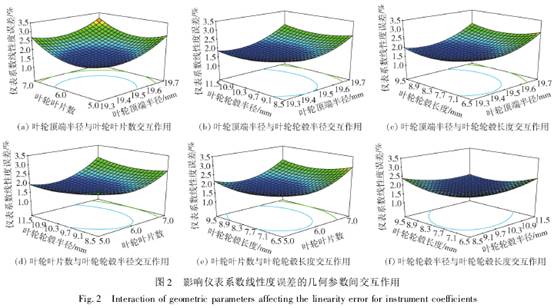
從圖2(a)~(f)可形象地看出影響儀表系數線性度誤差的幾何參數間交互作用。比較圖2各個分圖可知,葉輪頂端半徑R1對儀表系數線性度誤差的影響最為顯著,表現為曲線最陡,其余因素影響大小順序為葉輪葉片數N1>葉輪輪轂長度Lh>葉輪輪轂半徑R。這也與表5的方差分析結果相吻合。
使用DesignExpert軟件在表3變量的高低水平范圍內尋優,以葉輪葉片數是整數為前提,取其中一個最優組合進行CFD仿真計算,并與顯著因素的響應面回歸方程預測值進行比較,比較結果如表6所示。可以看出,對于優化后的流量計模型,其儀表系數線性度誤差擬合公式的預測值與CFD計算值非常接近,誤差僅為0.6%,說明響應面法可以很好地用于渦輪流量計結構優化。
3.2次顯著影響參數的正交試驗設計
在對顯著參數進行響應面優化后,選擇葉輪導程L、前導流件長度H、導流體葉片數N2、后導流件長度H2這4個次顯著影響因素為自變量,以流量計線性,度誤差為響應值進行正交試驗設計,根據因素和水平數選擇正交表L9(34),一共9組仿真計算模型,因素與水平見表7。
正交試驗結果與均值如表8所示,因素L對應的均值2最小,表明L取第二水平上的值時線性度誤差最小,同理可以得到H1、N2和H2的取值分別為:
第三水平、第二水平和第二水平,因此理論上的最優水平組合為L2(H)3(N2)2(H2)22。
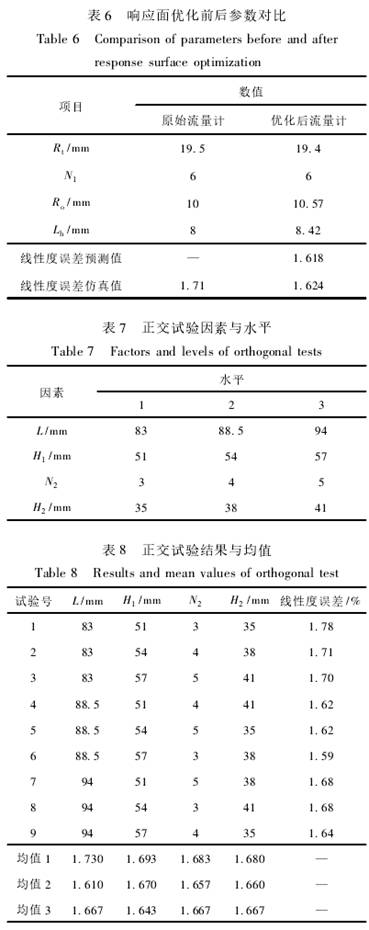
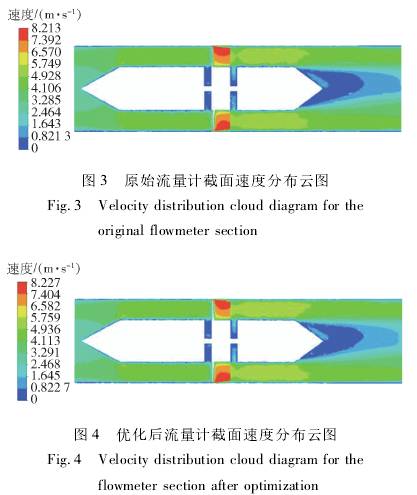
圖3和圖4分別為原始流量計與優化后流量計的截面速度分布云圖。對比圖3和圖4可以看出,優化后的流量計在后導流件.上下部分的流場速度分布較原始流量計更加均勻,說明優化后流量計的葉輪結構在流場中的旋轉穩定性更好,從而使得測量精度得到提高。
4試驗驗證
將優化前后的渦輪流量計在流量技術檢測試驗臺。上進行試驗,試驗裝置如圖5所示。試驗介質采用由機油和柴油按照一定比例混合的密度為887kg/m3、運動黏度為2.64×10-5m2/s的混合液,采用靜態容積法原理,利用泵為流體提供動力,流體經過流量控制閥和被測渦輪流量計后直接流回容積池中。分別選取2m3/h、4m3/h、8m3/h、14m3/h、16m3/h、20m3/h這6個體積流量點,通過計算機控制臺采集每個流量點下試驗流量計產生的脈沖個數N,從而得到渦輪流量計在6個流量點下的儀表系數K。試驗中每個流量點分別進行3次重復性試驗,試驗誤差均小于0.025%。

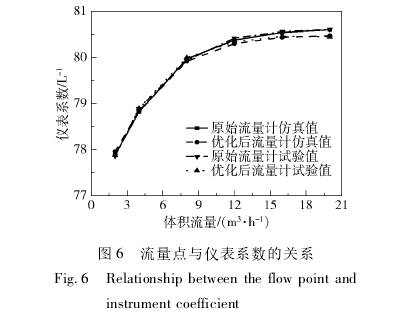
將原始流量計儀表系數與優化后的流量計儀.表系數進行對比,結果如圖6所示。流量計儀表系數CFD仿真值與試驗值吻合,證明了CFD仿真的準確性。對比原始渦輪流量計和優化后渦輪流量計儀表系數試驗值曲線得出,優化后的流量計在不同流量處的儀表系數變化情況較原來更為平穩。經計算,儀表系數線性度誤差由原來的1.71%下降到了1.59%,顯著提高了渦輪流量計的測量精度。
5結論
(1)Plackett-Burman設計分析表明,對渦輪流量計測量精度影響顯著的參數為葉輪頂端半徑、葉輪葉片數、葉輪輪轂半徑和葉輪輪轂長度,影響次顯著的參數有葉輪導程、前導流件長度、后導流件長度和導流體葉片數。
(2)運用Box-Behnken設計方法對篩選出來的顯著影響參數進行試驗設計,建立了渦輪流量計線性度誤差的多元回歸模型,并檢驗了預測模型的擬合度。結果表明,回歸模型對實際情況擬合較好,能夠運用響應面法對渦輪流量計結構參數進行優化。
(3)在響應面法優化的基礎上,對篩選出來的次顯著影響參數進行正交試驗設計,得到了最優結構組合。試驗驗證結果表明優化后的渦輪流量計測量精度得到了顯著提高。
以上內容源于網絡,如有侵權聯系即刪除!











