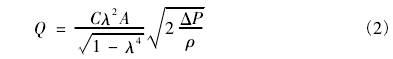目前,在各種工業生產中流量的測量非常重要,因此各種各樣的流量計層出不窮。壓差類的流量計由于價格較低,使用的經驗豐富,經過長時間的研究,精度越來越高,所以應用非常廣泛”。其中雙向內外管壓差流量計具有對流體的擾動小和獲得壓差信號大的優點田,但需要對雙向內外管壓差流量計的結構參數進行進YI 步的優化。影響雙向內外管壓差流量計性能的參數有很多,以往的研究大部分是對節流件的1個或2個結構參數進行同時優化,不夠全面印,如果對3個及以上結構參數同時優化,便需要進行大量的仿真工作,為提高效率,對仿真軟件進行二次開發。傳統的仿真軟件FLUENT難以滿足需求,而COMSOLMultiphys-ics仿真軟件可以導出M文件,在MATLAB中運行程序可以自動仿真并提取數據,二次開發難度低甲。如果COMSOL的仿真效果達到要求,那么在雙向內外管壓差流量計的仿真中,COMSOL仿真軟件便可取代FLUENT.
1流量計原理
雙向內外管壓差流量計的基本結構如圖1所示。安裝節流件的管道直徑選為32mm。雙向內外管壓差流量計節流件的長度對流量計的性能影響可忽略,為了方便測量,將節流件大管長度定為30mm,節流件的厚度定為2mm。
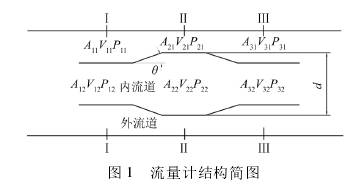
根據連續方程和伯努利方程5的原理可知,流體在通過節流件時,在I-I平面,外流道流體體積壓縮,流速增大,流體壓力減小,而內流道流體擴散,流速減小,流體壓力增大;在II-II平面,內外流道比較平穩,流速和壓力都趨于穩定:在亞一I平面,與I-I平面情況相反,外流道擴散,流速減小,流體壓力增大,而內流道流體壓縮,流速增大,流體壓力減小。如此--來,在II-II段節流件內外就會形成最大的壓差:
△P=P內一P外(1)
式中:△P為內外壓差;P內為內測點的水壓;P外為外測點的水壓。
與傳統壓差類流量計的測量公式類似,流量Q的計算公式為:
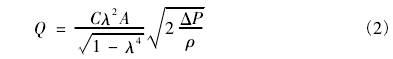
式中:C為流出系數;A為流道截面積,m2;λ為等效直徑比;ρ為流體密度,kg/m3。
影響流量計測量JINGDU 的主要因素是水頭損失。水頭損失包括沿程水頭損失和局部水頭損失。局部水頭損失是指因局部邊界急劇改變導致水流結構改變、流速分布改變并產生旋渦區而引起的水頭損失。沿程水頭損失是指在固體邊界平直的水道中,單位質量的液體自一斷面流至另一斷面所損失的機械能,這種水頭損失是沿程都有,并且隨沿程長度而增加。影響局部水頭損失的因素主要是節流件異徑比h、節流件的大管半徑R,影響沿程水頭損失的因素主要是擴散角θ。
2二次回歸正交試驗設計.
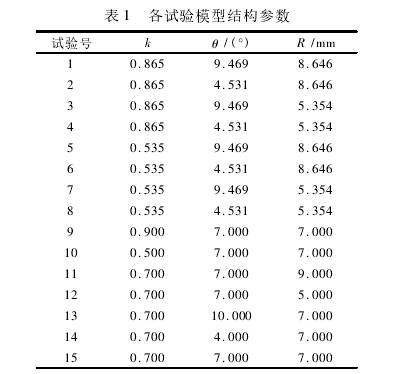
回歸正交試驗是在因素的合理變化范圍內選取有限個試驗點安排模擬計算統計,根據有限個試驗點建立具有一定可信度的回歸方程,當各個結構參數確定之后,可利用回歸方程進行估算見,。選擇優化的主要參數是異徑比k、擴散角θ和節流件的大管半徑R.采用二次正交回歸組合設計的試驗方法,首先設定3個控制參數的變化范圍:異徑比k為0.5~0.9;擴散角θ為4°~10°;節流件的大管半徑R為5~9mm。依據二次回歸正交試驗的設計原則,可以得到各組試驗的結構參數見表1。
3COMSOL與FLUENT仿真對比
利用SolidWorks建立三維模型,導入仿真軟件進行網格劃分。按照網格劃分的原則,參數變量變化梯度大的區域需要采用較為密集的網格劃分方法以提高精度,變化梯度小的區域采用較為稀疏的網格劃分方法以節省計算資源。節流件前后的流場劃分的網格稀疏,節流件周圍的流場劃分的網格密集回。FLUENT仿真軟件劃分的網格為非結構四面體,將整個流場進行網格劃分后,網格數量在30000左右,如圖2所示。COMSOL仿真軟件劃分的網格在靠近邊界的流場為六面體,其他區域的網格為非結構四面體,將整個流場進行網格劃分后,網格數量在100000左右,如圖3所示。兩種軟件的網格劃分方法相比較,COMSOL對流場的網格劃分更加正確。

雙向內外管壓差流量計的節流件采用對稱結構,流場雖然被分為內外兩個部分,但在節流件中部有一-段穩定流態的直管段,當流體流過節流件后,內外兩流道又合并為一個流道,其中流體的流.速和壓力逐漸穩定,在流場中并沒有過大的壓力梯度,所以湍流模型選擇K-ε模型。標準的K-ε模型現已經過許多改進,其中RNGk-ε模型來源于嚴格的統計技術,提高了精度和可信度,在FLU-ENT仿真中可以選擇RNGK-ε模型[10),但是在COMSOL仿真中只能籠統地選擇K-ε模型。
仿真介質選擇液態水,溫度20C,為不可壓縮流體,出口條件為outflow,試驗均在入口流速2m/s.的條件下進行仿真。在求解器的設置方面,兩種軟件均選擇“迭代或容差”的終止條件。
由于FLUENT與COMSOL軟件中均可設置對稱面,因此在構建三維模型時可以僅構建半個流場區域,以方便觀察截面.上的壓力分布。在仿真的后處理中,壓力測量點需要設置在流場穩定的區域,故計算壓損的前后壓力測量點設置在節流件的前后1個管徑距離的位置,計算壓差信號的兩個壓力測量點設置在節流件中心和外流道中心0。
4仿真結果和數據分析
對于雙向內外管壓差流量計而言,內外壓差信號大的條件下,壓損越小越好,故選取內外壓差信號與壓損的差值,即壓損差,作為雙向內外管壓差流量計的評價指標。按照前文設置的結構參數建立15組三維模型,分別利用FLUENT與COMSOL進行仿真,根據仿真結果,記錄內外壓差信號,將COMSOL和FLUENT仿真數據的差的絕對值與FLUENT數據的比值定義為誤差比,內外壓差信號數據對比見表2,用同樣的方法記錄兩種軟件仿真結果的前后壓損和壓損差,并計算出誤差比,數據對比見表3、表4。繪制的誤差比折線圖如圖4所示。
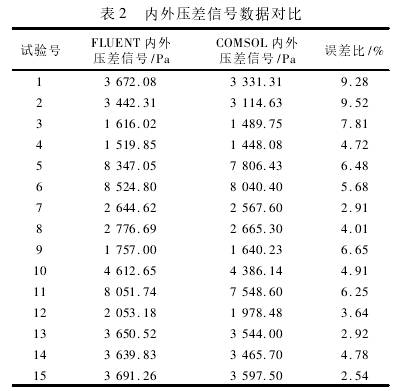
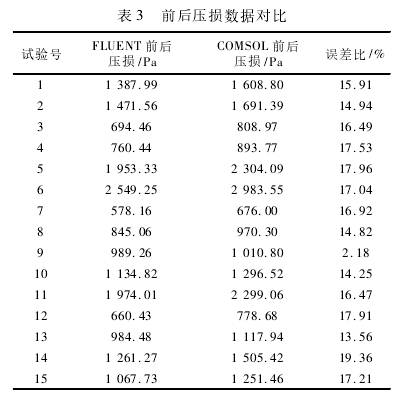
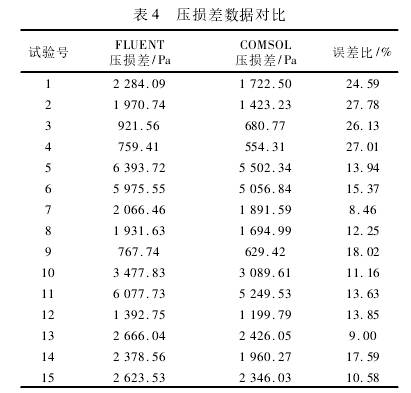
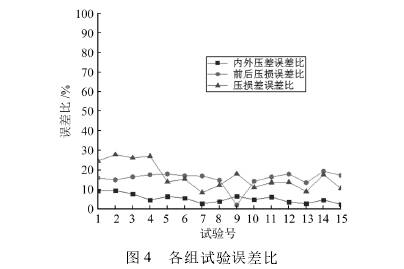
通過觀察表中數據可得到規律:COMSOL仿真數據與FLUENT仿真數據的誤差隨著FLUENT仿真數據的增大而增大。同時對比折線圖可發現各組數據的誤差比均維持在較低且穩定的水平。這樣的誤差比對于后續擬合二次回歸方程以及計算方程的最優解影響很小。
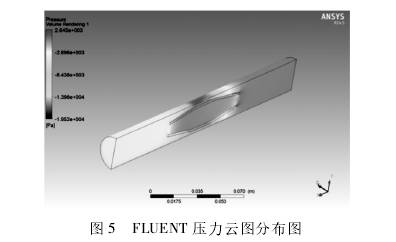
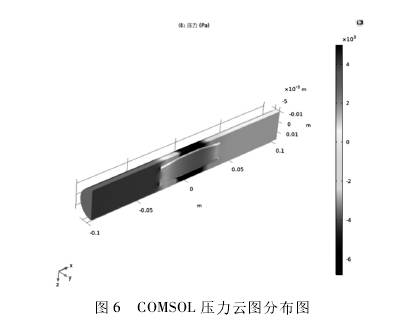
分別導出一組試驗的仿真壓力云圖進行對比,如圖5、圖6所示。由圖可知,壓力分布基本相同,COMSOL的壓力云圖更加立體直觀,視覺效果比FLUENT更好。
5結束語
以雙向內外管壓差流量計節流件的異徑.比h:擴散角θ和節流件的大管半徑R3個結構參.數為優化目標,設計了二次回歸正交試驗,分別用FLUENT和COMSOL進行仿真、記錄數據。通過COMSOL仿真所得的數據與通過FLUENT仿真所得的數據相比,雖然有浮動,但是誤差比卻維持在一個較低且穩定的水平,因此,使用COMSOL代替FLUENT進行雙向內外管壓差流量計的仿真。COMSOL的仿真過程可保存為M文件,方便利用MATLAB對COMSOL進行二次開發,對雙向內外管壓差流量計更多結構參數進一步優化。
以上內容源于網絡,如有侵權聯系即刪除!