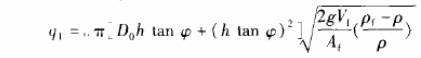摘要:為深入研究
金屬管浮子流量計的工作機理,采用計算流體力學和流體力學中湍流模式理論,對金屬管流量計流場進行了數值仿真研究,獲得了低黏度流體介質中浮子受力及浮子在受力平衡下的流量.數值模擬與物理.實驗標定數據的對比表明,模擬計算的流量最大滿度誤差為5.4695%,平均滿度誤差為2.4731%,說明數值仿真模型能滿足金屬管浮子流量計設計的需要.
金屬管浮子流量計是一種傳統的變截面流量計,具有結構簡單、工作可靠、壓力損失小且穩定、可測低速流體介質等諸多優點,廣泛應用于測量高溫、高壓及腐蝕性流體介質。目前,金屬管浮子流量計設計采用經典浮子流量公式計算,其中流量系數a受到浮子形狀和來流雷諾數等多種因素的影響,需要實驗標定來確定.該設計方法需進行大量的實驗,費用昂貴,周期很長,且獲取的數據有限.為深人研究金屬管浮子流量計的工作機理,筆者利用計算流體力學方法對金屬管浮子流量計進行數值仿真,通過構造仿真模型為研究金屬管浮子流量計的機理建立數值實驗平臺,優化傳感器的結構;同時為金屬管浮子流量計提供了低成本、短周期的設計方法.
1基本原理
1.1
金屬管浮子流量計的工作原理
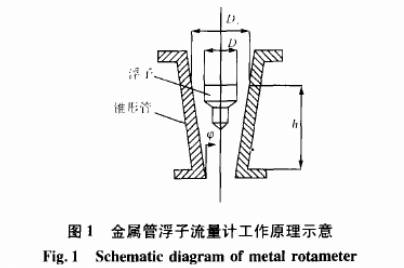
圖1為金屬管浮子流量計的工作原理示意.在垂直的錐形管中,放置-.阻力件,即浮子.當流體自下而上穿過錐管時,受到浮子迎流體積阻擋而產生一個壓差,從而對浮子形成向上的作用力,同時由于流體本身的黏性,對浮子產生黏性力,當這兩個力的合力大于浮子本身的重力時,浮子就會向上升,同時浮子與錐形管間的環形流通面積增大,流速減低,此時浮子對流體阻力作用減小.當浮子受到的力達到平衡時,浮子就會停留在某一高度.傳統的金屬管浮子流量計設計采用經典浮子流量公式2計算,即.
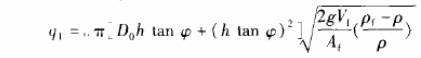
式中:q1為浮子流量計的體積流量;α為流量系數;D0為浮子最大迎流面的直徑;h為浮子在錐管中的垂直位置;?為錐形管夾角;Vf為浮子體積;ρf為浮子材料密度;ρ為流體密度;A1為浮子垂直于流向的最大截面面積.
1.2計算流體力學及其控制方程
計算流體力學(computationalfluiddynamics,CFD)是門利用計算機求解描述流體流動規律的控制方程組技術,涉及到流體力學.計算方法和計算機圖形處理等技術.為了簡便,以不可壓縮湍流流動為例寫出筆者使用的k-?模型通用形式的流體控制方程.在直角坐標系中.流動可由連續性方程和雷諾時均N-S方程描述,即
連續方程

k和ε由各自的輸運方程得到,對高Re數問題有

筆者的仿真模型建立在已有仿真實驗的基礎上”,并針對以往模型中存在的人口速度剖面為等值面這一不合理設置,給出合理的圓管人口速度剖面;同時按照實際流量計的構造,在流量計的人口與出口處加入導流架,從而提高了仿真結果的準確性.
2模型建立和數值計算
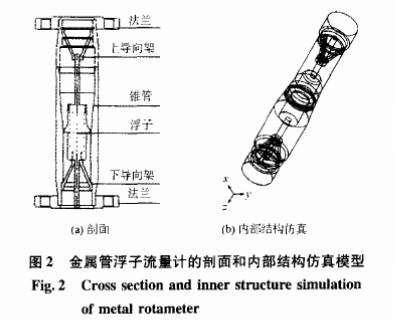
針對25mm1徑(DN25)浮子流量計內部機械結構進行流場計算和分析.金屬管浮子流量計結構剖面如圖2(a)所示.金屬管浮子流量計采用1Cr18Ni9Ti材質.流量計設計流量范圍為0.4~4.0m3,量程比為10:1,為了檢測錐管中浮子的位置.在浮子中安裝有水久磁鐵,同時利用網格生成器建立了浮子流量計內部結構仿真模型,如圖2(b)所示實驗所用的低黏度流體介質是在常溫下密度為998.0kg/m3、黏度為0.001002kg/(m.s)的水.金屬管浮子流量計內部流場是高雷諾數完全發展湍流流動,故采用湍流模式理論中標準k-?模型來計算.
2.1入口速度剖面設定
人口速度由經驗性光滑圓管湍流速度分布指數公式表示,即

為使構建模型能滿足不同口徑金屬管浮子流量計
的仿真結果,引人流量修正因子Cq,通過修正人口流
量來適應多種口徑金屬管浮子流量的仿真模型.
流量的修正公式如下:
qc=Cqq(9)
式中:q為實際流量;qc為修正流量;Cq為流量修正因子,對于25mm口徑的金屬管浮子流量計,Cq=1.13.
根據式(8)~式(11)編寫速度分布函數.圖3是q=4.8m3/h時金屬管浮子流量計人口速度剖面的仿真.圖中色標顏色由冷色調到暖色調表示速度由小到大,從圖中可以清楚地看到從邊壁到中心的速度是由小到大的非線性分布.


3仿真結果及分析
圖4給出了不同人口流量下,仿真計算得到的金屬管浮子流量計內部截面上的速度偽色圖.可以清楚地看到金屬管浮子流量計中流體在浮子周圍以及出入口的速度分布.隨著流量的增加,浮子在管中的位置上升,浮子與管道之間環隙變大,流體在管中的速度分布也隨之發生明顯變化.通過觀察偽色圖中的速度分布,并根據流體力學基本原理,可以初步判斷出計算所得結果是合理的.

根據物理實驗結果,仿真計算了浮子在錐管中某一高度處流體對它表面的壓力、黏性力和浮子重力Gf3項的合力Ff仿真結果中浮子所受合力結果見表2,合力向上為正方向.
由表2可知計算所得浮子在各位置的合力接近于零,趨于平衡,為驗證仿真模型所能達到的仿真精度,根據浮子只有在所受合力F,為零時才能平衡,又計算了浮子在各個高度保持平衡,即合力為零時,所對應的人口流量.表2還列出了數值計算與物理實驗所得流量的比較.并計算出仿真實驗的滿度誤差δs,即

式中;qs為數值模擬流量,m3/h;qp為物理實驗流量.
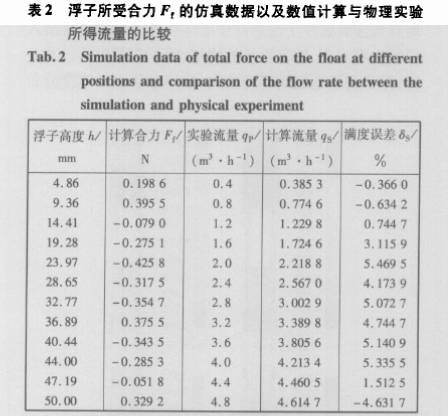
中表2可知,數值計算與物理實驗所得流量的最大滿度誤差為大滿度誤差為5.4695%,平均滿度誤差為2.4731%.利用本模型對50mm、80mm口徑金屬管浮子流量計仿真數據與物理實驗數據的比較結果也相當接近.表明筆者構建的模型得到令人滿意的結果.
4結語
通過計算流體力學方法對金屬管浮子流量計進行仿真,并對流場進行了定量分析,計算出浮子在金屬管中不同垂直位置的受力大小及受力平衡時所對應流量.仿真實驗結果與物理實驗數據相比,最大滿度誤差為5.4695%,平均誤差為2.4731%,表明筆者構建的金屬管浮子流量計數值模型能夠滿足低黏度介質金屬管浮子流量計設計要求,為金屬管浮子流量計傳感器結構進一步優化提供了可靠的數值仿真平臺。
以上內容源于網絡,如有侵權聯系即刪除!