摘要:通過對適合安裝于水平管道的特殊結構的水平安裝金屬管浮子流量計三維湍流流場的數值仿真及實驗研究提出一種基于計算流體力學的流量傳感器設計方法。流場仿真所需的模型采用GAMBIT來建立,通過FUNT軟件進行仿真,仿真過程中利用受力平衡控制計算精度。數值仿真結果和實驗結果比較當浮子受力平衡度誤差為9.5%時,流量誤差為0.944%,證實了仿真結果的準確性,同時利用流場仿真信息對流量傳感器模型做了進--步的優化。
1引言
金屬管式浮子流量計是一種傳統的差壓式流量計,為了適應部分管道的特殊要求,本文設計研究的浮子流量計是左進右出型的,其測量原理與經典的豎直型浮子流量計相同,但它是一種可以安裝于水平管道的特殊結構的浮子流量計。
一般對浮子流量計的經典研究是根據伯努利方程進行的,在推導浮子流量計流量測量公式時忽略了粘性應力項,而該項的作用實際上是存在的;傳統流量計的設計要通過實驗來檢驗和修正設計圖.紙,這樣不僅延長了設計周期而且增加了設計成本。基于.上述兩點原因,在設計水平式安裝浮子流量計時為了深入了解浮子流量傳感器的工作機理,引入了計算流體力學,即CFD2]技術,對傳感器流場進行數值模擬,通過對仿真及實驗結果進行分析來評價初樣設計,優化流量傳感器的結構參數,使流量傳感器的設計更加精確,并提高了設計效率。
2水平安裝金屬管浮子流量計的原理
2.1檢測原理(圖1)
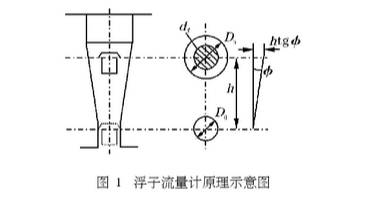
水平安裝金屬管浮子流量計的檢測原理與傳[1]統的金屬管浮子流量計相同,其體積流量公式為
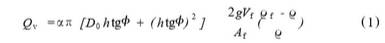
式中:Qv-體積流量;α-流量系數;h--浮子位置;φ-錐形管錐半角;Vf-浮子體積;Qf-浮子材料密度;Q一流體密度;Af-浮子垂直于流向的最大截面積;D。一浮子最大迎流面的直徑;Dh-浮子平衡在h高度時錐形管的直徑;df-浮子最大直徑。
2.2模型建立及其設計要求
浮子流量計傳統的設計方法是建立在式(1)的基礎之.上,在該方程中流量系數α是一個受很多因素影響的變量。對于本文所研究的水平式安裝浮子流量計,測量介質為20℃的水,設計要求流量測量范圍1~10m3/h,量程比為10:1,行程50mm,其流量系數x的經驗值為0.9~10。浮子位于41mm高處的傳感器三維流場模型如圖2所示。
2.3計算精度的控制
利用浮子組件受力平衡來控制計算精度。在FLUNT的受力分析報告中會提供指定壁面所受到的凈壓力Fy↑和粘性摩擦力Fm↑以及這兩個力的合力Fr↑。這三個力遵循下面的公式:
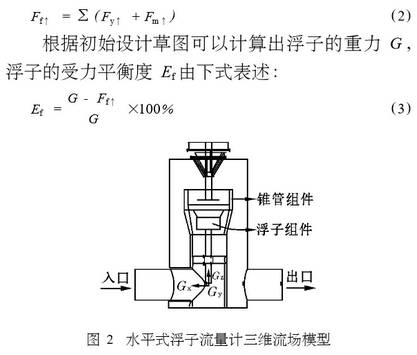
這里設定當浮子受力平衡度|Ef|<10%時,認為浮子受力達到平衡,此時停止計算。
3數值仿真
3.1網格劃分及邊界設定
針對傳感器的流場模型,選擇三角形四面體網格來進行網格劃分。如圖3所示為水平式浮子流量計浮子位于41mm高時的軸向網格剖分圖。
在進行邊界的設定過程中設定速度入口、壓力出口,并將導桿壁面設定為floatwalll,浮子壁面設定為floatwall2,除浮子組件和導向環外的空間設定為fluid。
3.2FLUNT計算條件
模型建好以后輸出.msh文件,利用FLUNT進行仿真,FLUNT中相應計算條件如表1所示。
其中流體介質的屬性:密度998.2kg/m2,粘度0.001003kg/ms,定壓比熱4182J/kg.K,熱導率0.6W/m.k.速度入口采用的是平均速度,針對浮子位于41mm高的模型計算達到平衡時的入口條件,如表2所示。

3.3仿真過程
水平式浮子流量計三維流場的仿真過程如圖4所示。該過程需要解釋的幾點如下所示:
(1)因每個模型入口流速的準確值未知,是根據經典流量公式計算的一一個假設的流量,因此仿真最終結束的判斷依據為浮子受力平衡的程度,即通過檢查仿真結果,對浮子進行受力分析,距離受力平衡點誤差小于10%時,認為達到計算精度,仿真計算結束。當誤差大于10%,首先考慮改進該模型的網格精度,如圖4中的左側方案1;當網格精度改進到一定程度后誤差仍大于10%,可修正入口條件.(主要指入口流速,其余條件可相應計算調整),如圖4中的右側方案2,直到滿足計算精度。
(2)利用SMPLE算法計算時,每次計算迭代次數為500次,當不足500次SMPLE算法就已經達到收斂精度(10“)時,程序自動結束,此時可檢查計算結果;當迭代次數大于500次仍未收斂時,停止計算,此時需重新檢查網格狀況和邊界設定,進行網格的合理剖分和邊界的合理設定。實踐證明,網格布置的恰當與否會直接影響收斂速度和收斂結果,不合理的網格布置將導致計算發散或者結果不正確。
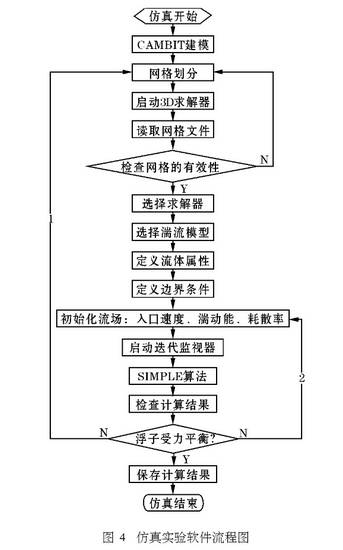
(3)迭代前首先打開監視器,監視X.Y、Z三個方向的流速以及k方程和c方程的收斂狀況,實踐證明,即使未達到預計的迭代次數,若在監視器中已出現明顯的發散現象,可強行中止本次計算。
4仿真結果及實驗結果分析
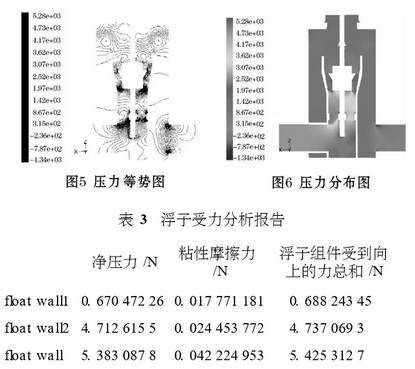
4.1壓力場分析(圖5.圖6)
比較壓力的絕對值可以看到:浮子底部左右壓力不對稱,這種不對稱現象的存在使得流量比較大時浮子會出現抖動。
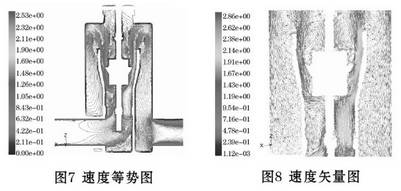
4.2速度場分析(圖7.圖8)
據圖分析如下:
(1)據顏色分辨出環隙流通面積最小處及下游靠近錐管壁的流場速度最大,前者是流通面積減小導致速度增大,后者則是因為流場方向的改變而引起的,特別是此處可能產生旋渦,導致有效流通面積減小,流體被擠向管壁,使得此處速度增大。
(2)流場下游,外直管左下角速度較小,主要是.因為流場的出口在右邊,由于出口壓力小,流體流動都趨向出口。
(3)浮子的最小截面處,流場速度存在較大的變化。
4.3浮子受力定量分析
從FLUNT的受力報告中可以得到如表3所示數據,根據設計初樣給出的浮子材料及尺寸結構,可得浮子重力為5.995146N。根據仿真結果,浮子在Z方向上的合力為5.4253127N。根據受力平衡度誤差分析公式可得,1E,|=9.5%,小于設定值10%,認為浮子受力達到平衡。
4.4物理實驗及結果分析
為了進一步驗證傳感器流場仿真結果,需要進行物理實驗。按照設計圖紙加工設計模型,加工完后,配上流量顯示儀表,在標準裝置上進行標定。標定方法利用標準表法,標準表選擇渦輪流量計(精度0.5級)。結合仿真流量數據、物理實驗數據與根據浮子流量經典測量公式得到的設計流量數據進行比較可以得到表4。

5大流量下流量傳感器結構的優化及改進結構后的仿真
由上述對壓力場的分析可知浮子組件受力不平衡,物理實驗也表明在大流量下會出現流量計振動的現象,這是由于傳感器流場出現了變化。從流場的速度分布圖可以看出,浮子組件的右邊速度特別大,其原因有前流場引起的,也有后流場的因素,由于傳感器的出口在右邊,所以流體有向右邊流的趨勢。另外,由于浮子組件前直管段有個直角彎,容易產生二次流,對浮子組件的受力也有很大的影響。所以,要減弱振動,解決的根本方法就是改變傳感器結構參數、優化流場、使浮子左右受力差盡量減小。
根據上述分析下面對水平式流量傳感器的結構提出幾點優化方案:
(1)加入整流器,以消除或減小旋渦的產生,同時調整流速的分布狀況。
(2)將前流場的直管連接改為彎管連接,減少旋渦的產生,順滑流體的流動,使傳感器有比較平穩的前流場。
(3)延長前直管段。這里提及的直管段指錐管前的垂直直管段,這也是為了使流體在通過整流器后有比較長的緩和段,使流場接近充分發展的流速分布。
改進結構后的仿真結果如圖9、10所示,據圖分析如下:
(1)改進結構后流場的壓力分布得到改善,浮.子組件受力接近平衡,但是,由于整流器的引入,導致了整流器前后壓差增大,帶來比較大的壓損。
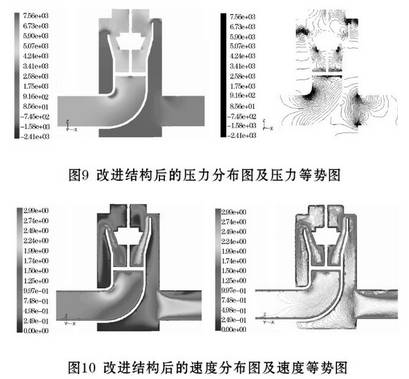
(2)改進結構后流場的速度分布比較均勻,特別是使浮子組件周圍沒有太大的速度差,同樣由于整流器的使用,也使浮子組件的前流場更加復雜。通過物理實驗也證實了這幾種優化方案可以有效的減少浮子左右受力差,穩定浮子。
6結論
由上述數據分析可知,對于浮子在41mm高處,時的三維湍流流場進行仿真可得到設計要求的流量上限值。此位置處浮子受力平衡度誤差為9.5%,傳感器物理實驗獲得的示值刻度流量與通過湍流數值模擬進行流場仿真實驗獲得的仿真流量值較為接近,仿真流量誤差為0.944%。本文利用浮子受力平衡度誤差法確定仿真計算精度獲得了較為理想的效果,即仿真過程無需過分強調浮子受力平衡度誤差的減小,仿真流量誤差即可得到令人滿意的結果。
理論分析和實驗研究表明,這種設計方法不僅可以進一步地理解流體流動的機理和浮子流量計的測量原理,而且使流量傳感器的設計進--步得到優化,使流量測量的靈敏度和精確度得到明顯的提高。此外,對流場的數值仿真與實驗研究也是分析、解決流量計其它問題的一-種有效方法。目前基于這種方法設計的水平式金屬管浮子流量計已經投入市場,現場,反饋這種流量計性能穩定,精度可靠。
以上內容源于網絡,如有侵權聯系即刪除!







