摘要:电磁流量计在测量浆液时，会受到浆液噪声的干扰,这种干扰是影响流量测量等指标的主要影响因素。由大量实验得知,浆液噪声符合1/f噪声特性,通过对1/f噪声的理论分析和数学计算,可以得到浆液噪声的数学模型。最后综合浆液的物理特性,可以得到参数可控的浆液噪声的仿真模型，该模型对噪声和电磁流量计设计都具有一定的实际价值。
浆液型电磁流量计的测量通道是一段段光滑的直管段,不会堵塞,非常适用于测量含有固体的固液两相流体，且电磁流量计在检测时不会带来压力等外力作用,所以节能效果好"。电磁流量计采用法拉第电磁感应定律作为设计原理，测量的体积流量基本.上不受流体的密度、温度、压力、粘度和电导率变化的明显影响,且其口径范围选择余地大,流量测量范围宽,也可用于测量具有腐蚀性的液体。
电磁流量计在测量液体时，两个电极与被测液体相接触,这样可以更正确地测量由于外加激励而产生的电荷偏移。流速为V的流体在外加磁场的情况下,切割磁力线,向两个电极方向移动,形成电势差E。但是在接触过程中,被测液体中混合的大小质量不均的固体颗粒在流体运动中，随机的冲撞电极，使得输出信号出现频繁的跳动,这种现象叫做浆状流体噪声，即浆液噪声。
1.1/f噪声的宏观解释
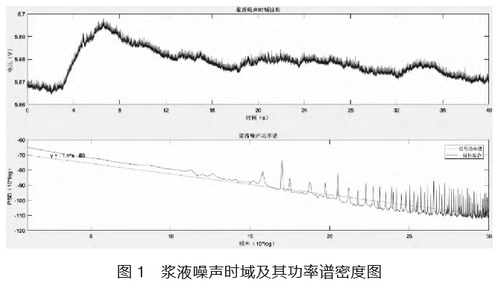
浆液内部含有大量的纸浆或砂浆等大小不均的固体颗粒,浆液流动时,这些颗粒会冲撞到电磁流量计的测量电极上,使得测量电极产生一个突变信号，大量的突变信号扰乱了正常的测量信号,原本应该平滑的感应电势叠加.上噪声,使得流量测量产生偏差'5]。将浆液噪声从流量信号里抽离出来,并从频域的角度分析可知,浆液噪声的功率谱密度符合1/f噪声特性，即信号的功率谱能量分布和频率成反比。功率谱分析表明浆液噪声的频率分布很宽,干扰的增益随着频率的升高而降低。图1为不含流量信号的浆液噪声时域图及其对应的功率谱密度图。
对于1/f噪声的研究,现阶段常用的有两种方法:一种是,首先产生随机白噪声,再把白噪声通过-一个高通滤波器经过滤波的噪声可以近似看作是1/f噪声;另一种是,用状态机的方法经过复杂的运算得到，或者用--种需要复杂方法的模型得出1/f噪声。
2.1/f噪声的统计解释
1/f噪声在很多自然系统中都有出现，近些年来越来越多的人都试图用数学分析的方法解释这种现象，但是所有的研究都.还未达成统一,但是有一个共性是公认的,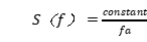
.下面是本文对1/f的一种解释。
则浆液冲撞电极的随机过程为计数过程，若N(t)表示时刻t为止累计的质点数量,则此过程满足以下条件:
1)N(t)≥0;
2)N(t)是正整数;
3)若s<t,则N(s)<N(t);
4)当s<t,N(t)-N(s)等于区间(s,t]中质点的数量。
由此可知,浆液冲撞电极产生的噪声，符合泊松过程,定义为:
其中n是平均脉冲率,三角方括号表示总体均值。这个功率谱的图形，在原点处近乎平直,然后经过一个过渡区,在高频处与1/λ2成比例!
但是这并不能细致的刻画1/f噪声的特性,它还和λ有关。设过渡区的两个端点值为λ1和λ2,则功率谱表达式为:
其中,K是与流速、浓度以及浆液颗粒形状有关的系数;a是表征噪声1/f特性的系数，通常1<a<2;S(w)为噪声序列中噪声频率f的统计幅值;T是浆液颗粒冲撞电极的间隔时间。
假设y=log10,S(ɷ),b=log10,K,kX=a*log10T,则统计功率谱在对数坐标系下,可将浆液噪声等效成Y==b+kX。Y正比于统计幅值,b正比于流速和浓度,k为浆液固有系数,表征不同种类的浆液。
浆液噪声的幅值VA符合高斯分布，且高斯分布的均值μ和方差σ与b和k有关。即高斯分布的均值增大，等效直线斜率增大，截距减小;高斯分布的方差增大,等效直线斜率减小,截距增大;幅值倍数增大,截距增大。
4实验验证
根据以上关系,设计一种浆液噪声Msury,此噪声由功率谱统计特性拟合的直线符合斜率为k=-1.9,截距为b=-52。噪声各频段斜率相近,整体波形随机曲折。
设△=1.37*10-3(s),n=30,mj=100,由以上构造方法可得时间序列Ndis，将离散的时间点Ndis线性化，即时间累积得到
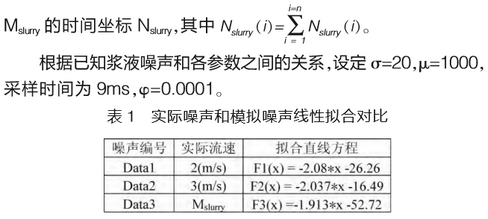
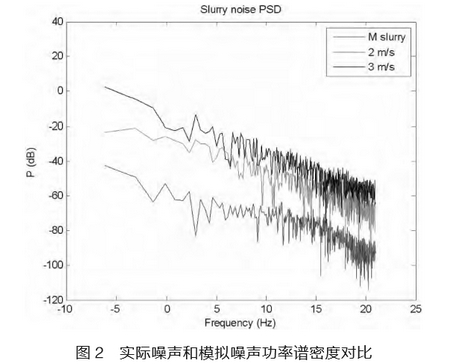
实验结果如表1,Data1和Data2为实际噪声测得的数据。
5结束语
通过分析浆液噪声,可以得到以下结论:.
1)根据浆液噪声的频谱特性的分析,此模型可用于在--定.频谱范围内近似代替实际浆液噪声;
2)浆液噪声在对数坐标下，呈现1/f的特性,浓度增加或者流速增加,曲线上移,浓度下降或者流速降低,曲线下移;低频噪声能量高于高频噪声，高频段比低频段丰富。
以上内容源于网络，如有侵权联系即删除!
