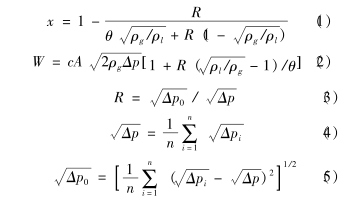1引言
对气液两相流量测量方法的研究,一直是国.内许多学者的工作重点。由于气液两相流量计量不同于单向流,因此对其流量的测量又分为单参数测量和双参数测量。其中比较典型的单参数测量方法有Lin模型、三通模型、Yue模型等,然而大多数情况,对气液两相流量计量需要双参数计量,如凝析天然气在输送过程中的计量问题,从而双参数计量对工业生产具有更重要的意义。
气液两相流量的双参数测量方法较多,按其测量方法大致可分为分流分相法、单相流量计组合法、软测量方法、利用差压脉动特性测量法。其中利用差压脉动特性测量法,是由单一孔板节流件,完成的双参数测量,这在国内众多双参数测量方法中是比较有特色的。但由于标准孔板的节流损失较大,而且孔板锐边易磨损和堵塞等缺点,限制这一方法在某些领域的应用。基于以上原因,本文对标准孔板进行了改进,并结合此测量方法,实现了汽液两相流量双参数测量。
2流量测量理论模型
2.1测量模型1
气液两相流量双参数测量模型为:
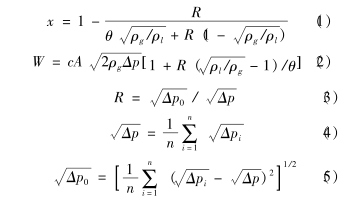
式中x一干度
A一孔板流通面积,m2
W一质量流量,kg/h.
g、l一气相、液相
ρ一密度,kg/m³
C一流出系数
√△p一孔板两侧的压差方根
θ一孔板的相分离系数,是ps/pt和孔径比β的函数;由试验确定
√△p0一压差方根噪声幅值
2.2测量模型2
根据文献01],申国强在总结各种流型下的
孔板压差数据得出:

同样运用单一-节流件,完成了气液两相流量的双参数测量。
2.3.2种测量模型对比分析
对比两种测量方法可以看出,虽然它们表达式不同,但都是通过压差脉动特性得出的测量模型,测量机理是相似的。结合式(2)和式(11)整理得:
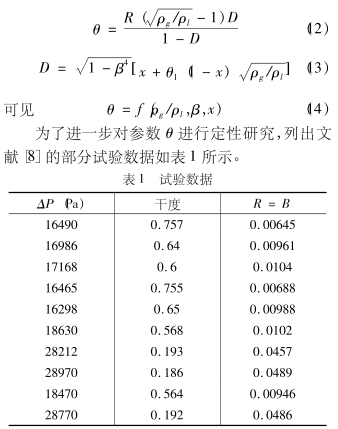
因为式(3)和(10)有着非常相似的数学表达式,根据数理统计知识可知它们是有联系的,图3可知,这两张图的中的R和x及B和x的对应关系基本一致,所以由B代替R时,认为它会影响θ的取值但不会对其变化趋势带来过大的波动。鉴于本文是研究θ值的影响因素,这里假设R=B。如果按照文献(10)的方法,那么在此试验数据的范围内参数θ应为一定值。通过式(1)计算得到的θ值,以及用此测量值计算的干度值和相对误差如表2所示。
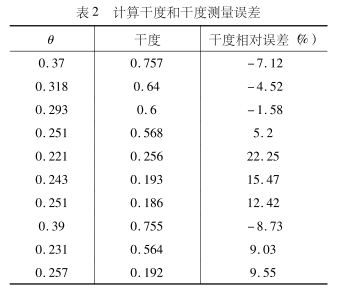
观察表2可以看出θ的测量值并不是一-定值,而且应用θ的平均值代入式(1)得出的干度测量相对误差很大,根本满足不了工业生产的要求。但是在表2中发现在干度大于0.6时,θ的取值和干度小于0.6时的取值相差很多,但在各自的区间上θ的变化并不剧烈。通过对比文献01]中的图4和文献{14}中的图3可知,在干度介于0.6两侧时R和x及B和x的函数关系明显不同。于是,从新以干度0.6为分界线分别求θ的平均值,然后根据式(1)求得干度相对测量误差≤±6.2%。经过以上分析可以得出,文献[7]的测量方法是正确的而且在干度变化不大的情况下,θ的取值基本不受干度的影响。在文献10]中同时给出了√△Po和σ(√△P)在本质.上无区别的结论,因此测量方法不仅适用于孔板,对其它节流件仍然适用。根据两种测量方法的机理知,文献8]的测量模型应用于其他节流件也是适用的。而且由式(10)和文献11]中的图4可以看出,这种计量方法相对简单,在干度小于0.2时B和x基本是线性关系。这对于气液两相流量测量仪表的实现是非常有利的。所以运用此方法,并且更换节流件,完成单一节流件的气液两相流量双参数测量是可行的。
3锥形孔板的设计
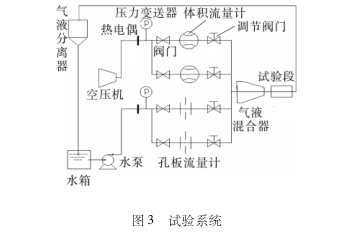
对于差压式流量计来说,不同节流件的选取,直接影响其性能的好坏。作为常用节流件的标准孔板,由于其易于安装,生产成本较低等优点,导致目前国内大约70%的差压式流量计是以它作为节流件。但随着能源问题的出现,因为其结构的原因导致节流损失较大,越来越多的行业已经放弃了它的使用。如图1示出孔板改进前后流体流动方向对比。从图1中可以看出通过对垂直入口进行改进后,得到的孔板流出特性较好,具有防堵、节流损失小等优点。为了确定的入口锥.角,本文通过数值模拟的方法,对3种不同入口锥角的锥形孔板进行管内数值模拟。得出不同入口锥角的锥形孔板流出系数与雷诺数的关系图,如图2所示。从图中可以得出,随着入口锥角的减小,流出系数会增大,但增大趋势减弱。根据文献[15],一味的增大流出系数和减小压损,可能会造成计量精度的下降。
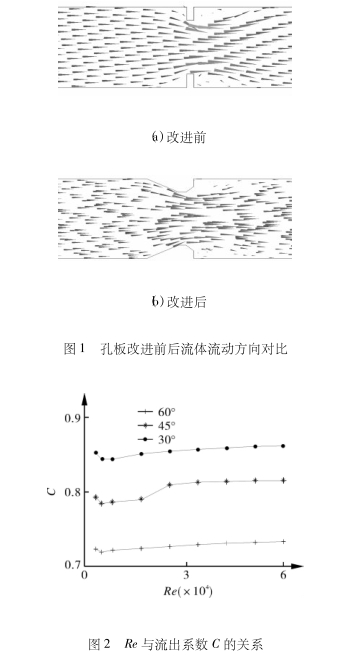
最终确定以入口锥角为30°的锥形孔板为试验节流件。
4试验部分
4.1试验装置及试验条件
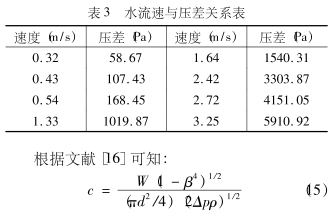
试验是在东北电力大学气液两相流试验台上进行的,试验介质为空气和水,试验锥形孔板孔径比为0.67,前锥角等于30°,后锥角等于45°,过度平台长度为2m,管径d为30m,取压方式为,环室角接取压。试验流程如图3所示。试验参数范围:压力:209~260kPa;质量含气率:0.00021~0.028;温度:13~15℃;总质量流量3224~11546kg/h。采样频率为256Hz,采样时间16s。
4.2试验结果与分析
根据测量方法,要想进行流量的测量,首先得求出锥形孔板的流出系数和林氏模型θ1的关系式,表3是以水为介质得出的试验数据。
得出锥形孔板流出系数值为0.84。对比图2可以看出,这一结果和模拟结果很相近。说明数值模拟方法在改进节流件性能时有很好的指引效果。同时在本试验条件下,得出了50组气液两相流量测量数据。根据林氏模型θ1是气液密度比.的函数,基于本试验温度变化较小,所以以压力对θ1进行多项式拟合得到:
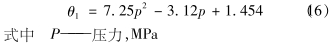
通过测量50组试验数据的B和x,得到B和x的关系,如图4所示。由图4可以看出,B和x呈现单值函数关系,而不是线性关系,而且B的取值和文献[1]中的相比波动很大。出现这一结果的主要原因,应该是本文的试验范围的不同。由于在干度大于0.1时,气液两相流动主要呈现的是环状流,此种流型下,液相会在管壁处形成液膜,而夹带液滴的气相在管道中部高速流动,导致了汽液两相流动过程的压差波动性降低。而在本文试验过程中,汽液两相流动随着干度的增大,主要表现出气泡流、塞状流、弹状流、波-弹混状流。根据B的计算式可知,当压差波动越剧烈时B的取值越大,因此流型的变化是导致文献11]和本文结果不同的根本原因。
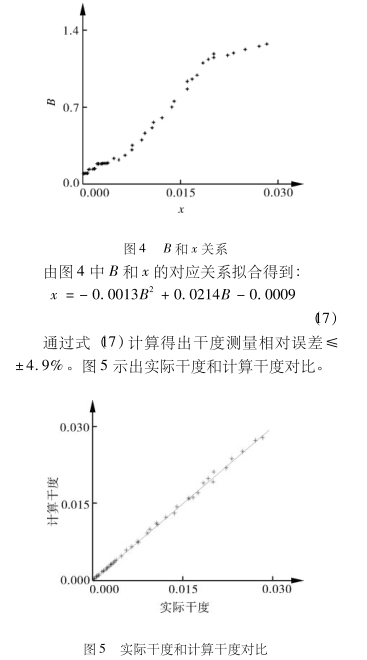
干度测量误差的形成,可能是由于汽液两相流动具有一定的随机性,即使干度相同时,其它参数如:压力、温度等的微小变化也可能导致局部流动型态的变化,从而引起压差脉动幅值的变化。所以对于同一千度也会产生测量误差。另外文献01]中的测量方法认为压差瞬时参数与时均参数的规律相同,而并未严格证明,这也可能是测量误差形成的原因。
由式(11)、(16)和(17)计算得到的流量测量相对误差≤±9.7%,如图6所示为计算流量和实.际流量对比。
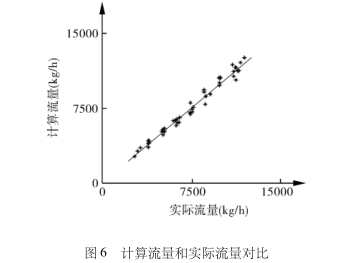
本文是通过压力对参数θ1拟合的,并不是严格以气液密度比来拟合θ1,,另外本文试验条件干度小于0.1,气液两相流动的型态变化较多,而林氏模型较适合用于干度大于0.1的试验条件,这可能是流量测量误差较大的原因。若能基于流型来拟合θ1,测量误差是可以减小的。
5结论
(1)通过对2种测量模型的数学表达式及部分试验结果分析后,得出2种测量方法是有联系的,在较为合理假设基础上重新验证了模型1的正确性。由两者内在关系知,这也能间接证明模型2的合理性;
2)根据文献10]中模型应用范围推广的结论:,得出文献[8]的测量方法同样适用于其他节流件;
(3)结合数值模拟方法和试验研究,设计了--种节流损失小、防堵功能强的锥形孔板并将其应用到实际流量测量中;
(4)通过本文试验研究得到了文献01]中千度小于0.1时B和x的关系式,为此种测量方法应用范围的拓宽提供了参考依据;
(5)在试验条件范围内,借鉴文献11]的测量方法,同时,应用本文设计的锥形孔板,实现了运用单一节流件测量汽液两相流量的双参数测量。
以上内容源于网络,如有侵权联系即删除!