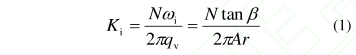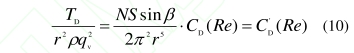摘要:涡轮流量计的精度受被测介质及其运动粘度变化的影响。使用体积流量和仪表系数无法从变粘度实验中取得形态-致且可预测的标定结果。应用量纲分析导出雷诺数和斯特劳哈尔数作为描述涡轮流量计性能的无量纲参数。通过改变丙二醇-水溶液的体积浓度得到五个不同运动粘度的介质,分别用于标定一台DN25涡轮流量计。对比结果表明,不同粘度下的标定曲线在雷诺数小于7400区域出现分离,标定数据最大相差0.9%。随着雷诺数增加,仪表系数中轴承阻滞部分的影响相对减小,标定曲线簇由分散趋于聚拢,标定数据差异小于0.1%。叶片表面的流动边界层发生层淌转捩时阻力的突变导致标定曲线出现驼峰,运动粘度越低,驼峰趋于平缓。轴承阻滞中的静态阻力部分是造成相同雷诺数下仪表系数差异的主要原因,这种差异随雷诺数减小而增加,所以,当校准介质和工作介质的运动粘度有显著差异时,涡轮流量计要避免工作在低雷诺数区域 。
0引言
涡轮流量计是一种可靠的,用于测量流体流量的仪表。石油、化工领域大量使用涡轮流量计测量输运天然气、燃料油和烃类流体的流量,涡轮流量计的精度对于涉及能源的贸易交接非常重要。自从1790年ReinhardWoltman使用第一台涡轮流量计测量水流量以来,涡轮流量计经历了许多变化和改进,仍然被认为是一种准确且稳定的工业仪表",在稳定条件下,液体涡轮流量计的精度可以达到0.1%,气体涡轮流量计的精度可以达到0.5%121。
通常情况下,计量技术机构或校准实验室使用某一种流体(一般是水)校准涡轮流量计,而实际被测对象常常是另外-一种介质。即使校准和工作场合中使用同一种介质,液体的运动粘度易受温度变化影响,涡轮流量计性能会有较大的差异,需要增加额外的校准工作。例如,在油品或烃类介质的贸易交接中,如果更换了管道中的介质或介质的物性发生较大变化,都要对涡轮流量计进行--次现场重新校准。
以往的研究表明,涡轮流量计在低粘度流体(1mm2/s及以下)和高粘度流体((50~100)mm2/s)下的标定曲线形态有很大不同4。虽然对此已有很多研究和报道[5),但粘度影响涡轮流量计性能的流体动力学机理仍未被完全理解161。已经发表的涡轮流量计物理模型大多基于动量和气翼理论,但这些模型都依赖于实验数据的修正,还没有一个经过广泛验证的物理模型能够充分解释涡轮流量计的输出响应以及标定曲线的变化细节。
近年来,借助计算流体力学(computationalfluiddynamics,CFD)模拟研究了流量计内部的流场,分析影响涡轮机流量计精度的因素,通过优化结构参数来提高流量计的性能。提出一种针对液体涡轮流量计叶轮的多参数定量优化方法,以减少粘度对传感器特性的影响。根据CFD软件计算得到的流场信息解释流体粘度变化影响传感器性能的机制。在其提出的数值模型中考虑了轴承阻力矩,通过CFD计算预测涡轮流量计的性能。通过CFD模拟分析了,上游整流件的结构参数对涡轮流量计性能的影响,并提出了整流件结构的优化方案。定义了一个表征叶轮叶片形状的结构参数,通过CFD模拟分析涡轮流量计内部流场,解释叶片结构对其性能的影响机制。
上述研究都是基于转子系统的力矩平衡,通过改变流体物性计算相应的流场信息,进而得到流量计的输出响应。相较而言,通过实验研究仪表系数和标定曲线的演化规律,人们能够更直观地了解仪表对实际工况的响应。本文基于动量方法的基本表达式,应用量纲分析导出雷诺数(Reynoldsnumber,Re)和斯特劳哈尔数(Strouhalnumber,Sn)作为描述涡轮流量计性能的无量纲参数。分别使用五种运动粘度((1.02~30)mm2/s)介质标定一台DN25涡轮流量计,实验数据揭示了受粘度变化影响的仪表系数在低雷诺数区域出现明显差异,以及由于层湍转捩时阻力变化所导致的驼峰形标定曲线在粘度影响下的分布规律。
1研究对象及其出厂标定数据
图1所示的是一台8个叶片的DN25涡轮流量计的转子结构。流量计的量程范围是(0.6~12)m/h。为了使该流量计适用于多种粘度介质,制造商在出厂标定时使用五种烃类介质,标定结果用体积流量qv和仪表系数K表示(如图2所示)。相对于低粘度介质,高粘度介质((28~-788)mm2/s)下的仪表系数与体积流量呈现高度非线性。标定曲线随粘度的改变出现偏移,流量越小,偏移量越大,以运动粘度v=1.09mm2/s的仪表系数为参考,体积流量qv=1.2m2/h时其余四个粘度的仪表系数分别偏移0.5%、2.6%、14.6%和50.3%,可见qv-K标定曲线并不适用,需要重新选择两个参数分别代表来流的标准值和流量计的输出响应。为此,对涡轮流量计物理模型的表达式作量纲分析。
2量纲分析
作为体积流量的直接体现,涡轮流量计的旋转角速度ɷ和通过流量计区域的流速V成正比。理想情况下的流量计仪表系数Ki是一个常数,由流量计的几何形状和尺寸决定,与实际流量或流动状态无关,即
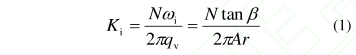
式中,A是流量计叶片进口处的流道截面积,N是叶片数,qv是体积流量,r是叶片边缘处的半径和轮毂半径的均方根,即平均有效半径,β是r对应的叶片角度。实际情况下,叶片受到的阻滞力矩T,使转子实际旋转角速度w低于理想角速度ɷi,于是,实际仪表系数K.为:

量纲分析的第一步是从所研究方程中确定合适的变量,第二步是选择π方程的基本变量,第三步是确定每个π表达式中基本变量的指数,最终确定关键的无量纲参数。式(3)中有f、qvr、B、ρ和Tr六个变量,.还有一个物性变量一动力粘度μ隐含在方程中,动力粘度影响流量计流道中的速度剖面分布,以及流体沿叶片表面和轮毂的流动阻力,所以,量纲分析需要使用七个变量。
从式(3)中选择的第一个变量是频率f,量纲单位是T';第二个变量是流速V,相对于体积流量q(包含面积单位),流速是一个更基本的变量,量纲单位是LT;第三个变量是平均有效半径r,这里使用更容易确定和标准化的流量计直径D代替,量纲单位是L;第四个变量是叶片角度β,这里使用一个简单的长度l代替,量纲单位是L;两个流体物性变量密度p和动力粘度u,量纲单位分别是ML-3和是ML-1T-1;最后一个变量是阻力矩T,量纲单位是M.L2T-2。
七个选定的变量中流速V、流量计的尺寸D和l决定了仪表本身的性能。流体物性p、μ和阻力矩T;影响仪表的实际性能。七个变量包含三个量纲单位(L、M和T),故选择三个变量(D、V和p)作为基本变量。四个π方程(7个变量-3个量纲单位=4个方程)如式(4)所示。

性能,故舍去。进一步转化T2得到关于仪表系数K的斯特劳哈尔数(Strouhalnumber,St)::

将雷诺数作为标定数据的横坐标,代表标准流量值,将斯特劳哈尔数作为标定数据的纵坐标,代表流量计对于标准流量值的输出响应。涡轮流量计出厂标定数据的Re-St散点如图3所示,流量计在不同粘度介质下的输出响应被重整为一条和雷诺数有关的曲线,而且在一个阈值(Re=16400)以上,斯特劳哈尔数变化范围小于0.5%。这意味着,即使校准和工作场合使用的介质粘度不同,只要雷诺数超过这个阈值,经过校准的流量计示值的不确定度仍然比较低。
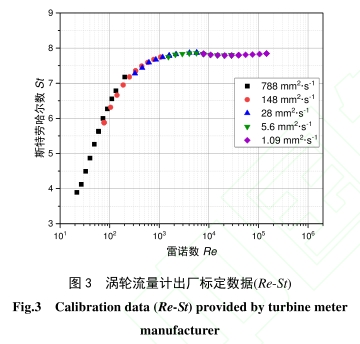
要指出的是,有些制造商(特别是北美地区)还提供了以罗什科数(Roshkonumber,Ro,表达式如式(9)所示)为横坐标,斯特劳哈尔数为纵坐标的通用粘度曲线(universalviscositycurve,UVC)14),
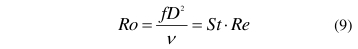
罗什科数是流体力学中描述振荡流的无量纲数,但是用于描述流量计的性能缺乏明确的物理意义,而且Ro-St通用粘度曲线与Re-St曲线的形态也非常相似,其优点是方便仪表用户使用。因为罗什科数不包含体积流量,当用户已知介质的运动粘度并且收到涡轮流量计发出的频率,由Ro-St通用粘度曲线直接得到经过标定的仪表系数。对于关注涡轮流量计性能的研究者、制造商以及校准实验室,Re-St曲线更加直观,不仅含有明确的物理意义,而且可以改善涡轮流量计标定结果的可预测性和一致性。
3实验装置与标定结果
3.1实验装置描述
某校准实验室的小型活塞式液体流量标准装置以丙二醇-水溶液为介质,将这台DN25涡轮流量计作为期间核查对象。装置使用压缩空气驱动的18L主动活塞作为标准器(如图4所示),最大流量260L/min,装置的扩展不确定度Ue=0.05%(k=2)。该装置有“运.行”和“返回”两种操作模式。在“运行”模式中,压缩空气被引入到气腔,以恒定的速度推动活塞向右移动,将介质排出液腔并通过被检流量计。光栅和线性编码器负责确定活塞的位移。当活塞完成一次行程后,进入“返回”模式。控制阀切换使压缩空气进入储液罐,推动活塞向左移动,直至液腔完全被介质填满。系统调整后,准备进行下一次检测。
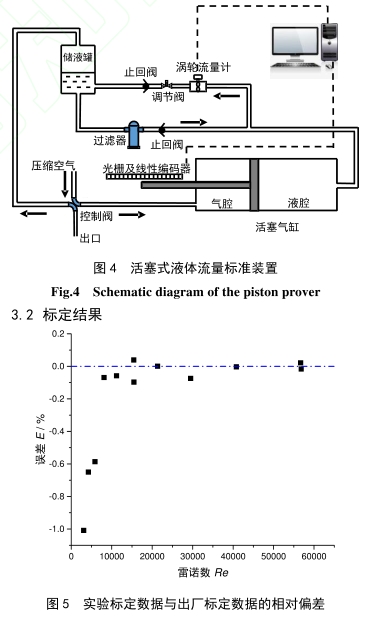
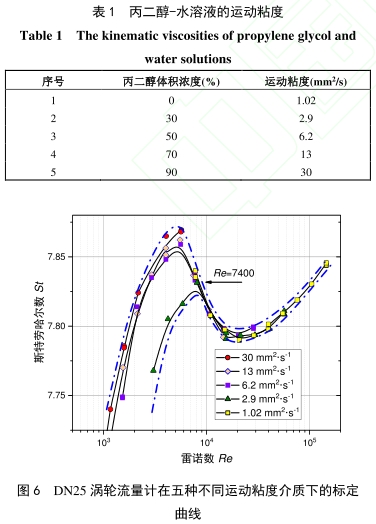
首先在运动粘度v=2.9mm2/s下标定该流量计,按体积流量设定12个检测点,所以每一点的雷诺数与出厂标定时雷诺数有一-定偏差(小于7%)。标定结果与流量计的出厂数据对比如图5所示,当雷诺数小于8000,两者的偏差大于0.6%,最大偏差为1%;当雷诺数大于8000,两者的偏差在0.1%以内。实验结果表明,在流量计量程的低区,即使使用粘度较低的介质,.出厂标定数据和实测结果的差异仍然较大。根据校准实验室的工作需求,配置了五种不同粘度的丙二醇-水.溶液(物理性质如表1所示,实验室环境温度(21~23)°C),重新标定流量计后,结果分别绘制成Re-St曲线(如图6所示)。不同粘度的标定曲线簇以Re=7400为界呈现出分散和聚拢两种特征,在聚拢区域,相同雷诺数下,不同粘度的标定数据两两之间的差异小于0.1%;而在分散区域,最大相差达到0.9%。由图3可知,在低雷诺数区域,斯特劳哈尔数随着雷诺数减小急剧下降,那么,不同粘度的标定数据差异会越来越大。以下将结合涡轮流量计物理模型分析上述特征。
4分析与讨论
Lee等15116基于动量和翼面方法推导出仪表系数的表达式(式(2))。参考Wadlow1I关于涡轮流量计的理论综述,将阻滞力矩表示为基于角速度与体积流量之比的仪表系数形式,即T:/(rpq.2),(i代表r,D或B)。由于各种气体的动力粘度差异很小,Lee等人将模型应用于气体涡轮流量计时,简化了轴承阻力矩的影响,并且认为轴承阻力矩在高雷诺数范围内几乎不变,于是式(2)仅包含流体粘性阻力矩Tp:
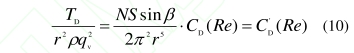
式中,S为叶片表面积,系数Cp(Re)是仪表几何参数和一个与雷诺数有关的无量纲阻力系数Co(Re)的乘积,而且,这个无量纲阻力系数取决于叶片表面的流动边界层是层流还是湍流,当发生层湍转捩时,叶片表面摩擦阻力急剧变化。忽略轴承阻滞后,流体对转子的粘性阻滞只和雷诺数有关,所以在变粘度实验中,.Lee的原始模型无法解释流量计的标定数据为何在相同的雷诺数下存在差异,并且形成分散的曲线簇。
Pope等18进一步扩展了Lee模型,将阻滞力矩Tr分成施加在转子.上的流体粘性阻力矩TD和轴承阻力矩TB,其中轴承阻力矩Ti包含三部分:(1)与转子转速无.关的轴承静态阻力矩(CB0);(2)几乎随转子转速线性增加的轴承粘性阻力矩(Capvo);(3)随转子转速的平方增加的,由轴向推力和转子系统的动态不平衡引起的阻力矩(Cr2ɷ²),其中CBi,(i=0,1,2),是仪表特定常数,令CBo/r2=CBi,得到:

式(12)~式(15)表明,在流体粘性和轴承阻滞的作用下,涡轮流量计的实际仪表系数不仅取决于雷诺数,而且受到密度、体积流量,运动粘度以及转速的影响,对于同一雷诺数,存在多个仪表系数与之对应,所以标定曲线簇出现分散。尽管随着雷诺数增加,式(13)~式(15)所代表的轴承阻滞趋于减小,但是转子转速也在增加,需要结合实验数据分析轴承阻滞中三个部分的变化趋势,寻找导致曲线簇分散的主要原因。(1)图7是不同运动粘度的轴承静态阻力部分随雷诺数的变化情况。虽然从式(13)可知其依赖于体积流量,但是实质.上,粘度差异引起轴承静态阻力数据相互分离,随着雷诺数平方级增加,轴承静态阻力部分迅速减小,对曲线簇分散所起的作用随之迅速减弱。.
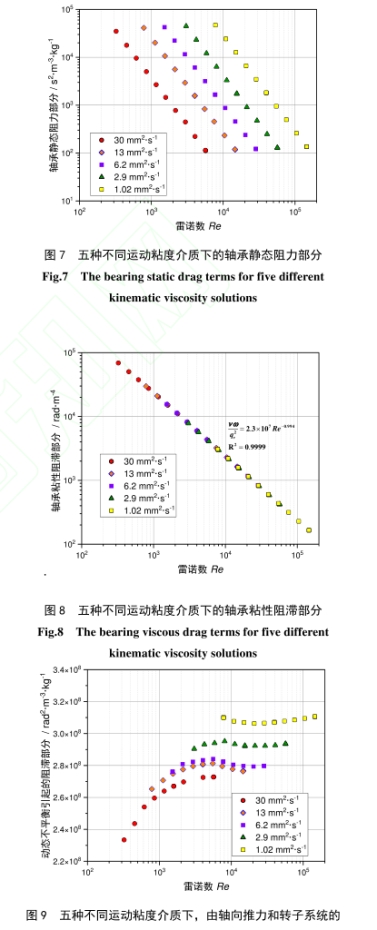
(2)如式(14)所示,将轴承的粘性阻滞拆分为两部分:如果第一部分o/qv成比例,各个运动粘度下的粘性阻滞将沿同一条曲线随雷诺数递减,否则,会出现多条随雷诺数递减的曲线。图8所示的散点及其拟:合曲线方程表明,各个运动粘度下的轴承粘性阻滞沿着一条近似于雷诺数倒数的路径递减,没有出现明显的散点分离,因而轴承粘性阻滞不是导致曲线簇分散的主要原因。
(3)图9所示的是轴承阻力中由于动态不平衡引起的阻滞,这部分阻滞由于运动粘度的不同存在明显的差异,由于该项随着角速度的平方而增加,所以差异不会随着雷诺数增加而减少。最终Re-St图中曲线簇趋于聚拢,说明这部分阻滞作用占比很小。在高雷诺数区域,不同粘度标定曲线之间存在的差异仍然保留了这部分轴承阻滯的作用。
由上述分析可知,轴承阻滞中的静态阻力部分在不同粘度下的差异是造成曲线簇分散的主要原因,分散特征需要具备两个条件:第一,除了雷诺数以外,轴承阻滞各分项中还存在受其他因素(例如,运动粘度)影响的成分:第二,由于轴承阻滞始终随雷诺数增加而递减,只有那些不受雷诺数抑制的部分得以保留其对分散特征的贡献。
需要指出的是,图6中Re=7400处的数据同时承载了两方面的信息:一方面,分散的曲线簇在雷诺数达到7400后聚拢于-一个狭窄的区域,表明轴承阻滞在不同粘度下的差异趋于减小,其在仪表系数中的作.用降低,仅和雷诺数有关的流体粘性阻滞成为影响仪表系数的主要部分;另-.方面v=2.9mm2/s的标定曲线在Re=7400形成驼峰,驼峰的形成与流动状态有关[19,直接影响涡轮流量计在有效测量范围的线性度。5个粘度下的标定数据覆盖了层流、湍流、和层-湍过渡区域。若以v=30mm2/s标定曲线作为层流的代表,以v=1.02mm2/s标定曲线作为湍流的代表,将4020≤Re.≤10000视为层流向湍流过渡区域。根据式(10),待定系数C(Re)和流动阻力有关,层湍转捩时,流动阻力突增导致仪表系数下降,标定曲线出现驼峰。Griffths和Silverwoodl2)通过锉掉叶片后缘的棱角改变后缘轮廓,提高叶片的旋转速度,使仪表系数上升,逐渐消除驼峰,这是因为流动边界层分离点位置发生变化导致阻力减少。由式(12)和(13)可知,在相同的雷诺数下,介质运动粘度越大,相应的仪表系数越大,高粘度介质的标定曲线位于低粘度介质的标定曲线之上。由于曲线簇随着雷诺数增加趋于聚拢,各条标定曲线在层湍转捩后,都将回落到v=2.9mm2/s曲线的驼峰点以下,所以,低粘度介质的标定曲线的驼峰曲率比高粘度介质小,而且发生层湍转捩时的雷诺数更高。实验中,量程的上限是12m³/h,v=30mm2/s标定曲线没有观察到明显的层湍转捩,而v=1.02mm2/s标定曲线在量程的下限0.6m³/h时已经是湍流状态了,这两条标定曲线都没有驼峰,于是,可以将Re=7400作为该流量计的特征驼峰点雷诺数。
由前述分析可知,尽管通过优化叶片或转子系统的结构减缓甚至消除驼峰,能有效改善仪表的线性度,但是,因为轴承静态阻力部分仅受介质的运动粘度和密度影响,优化结构无法减弱标定曲线的分离,所以,当校准介质和工作介质的运动粘度有显著差异时,不能使用特征驼峰点雷诺数以下的标定结果。
5结论
当液体涡轮流量计的校准介质和工作介质不同,或者因温度变化导致两者的运动粘度差异较大,若以体积流量作为计量单位,涡轮流量计会表现出显著的性能差异。应用量纲分析,从涡轮流量计的仪表系数表达式中导出雷诺数和特劳哈尔数作为描述涡轮流量计标定曲线的无量纲数,一台DN25涡轮流量计的出厂标定数据被重整为一条Re-St标定曲线。按照某校准实验室的实际工作需求,配置了五种不同粘度的丙二醇-水溶液作为校准介质,重新标定该流量计。不同粘度的标定曲线在低雷诺数区域有显著差异,标定点数据两两之间最大相差0.9%,随着雷诺数增加,差异减小至0.1%以下。分析结果表明,轴承阻滞在不同粘度下的差异导致曲线分离,其中轴承的静态阻力是主要.因素,随着雷诺数增加,轴承阻滞对仪表系数的影响减少,曲线簇由分散转为聚拢。轴承阻滞中,由轴向推力和转子系统的动态不平衡引起的阻滞效应也会导致标定曲线的分离,且不受雷诺数的抑制,因而曲线簇始终保留着少部分分散特征。
以往的研究通过优化转子系统的外型和结构,减小阻力,提高转速,增加小流量下的仪表系数,从而提高仪表的线性度21。标定曲线出现驼峰是因为随着流速的增加,叶片表面流动边界层由层流向湍流转捩时阻力突增,作为一种优化涡轮流量计性能的方法,改变叶片的结构轮廓能够减缓驼峰,从而提高仪表的线性度,但是不能减弱多粘度标定曲线簇的分散特征。所以,当校准介质和工作介质的运动粘度有显著差异时,涡轮流量计要避免工作在轴承阻滞作用显著的低雷诺数区域。特别是当介质的运动粘度较大(例如文中v≥13mm2/s)导致涡轮流量计主要运行在特征驼峰点雷诺数以下,如果输运管道中介质发生了改变或工作温度有较大差异,应当配置流量标准装置对涡轮流量计进行一次现场重新校准。
本文来源于网络,如有侵权联系即删除!