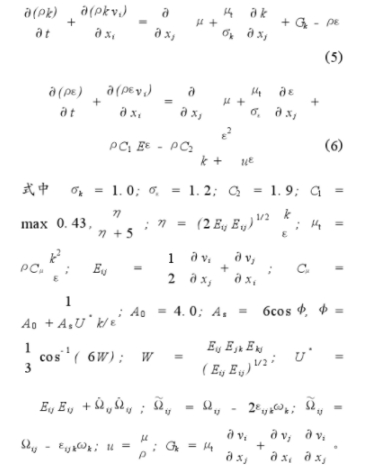摘要:为了深入研究涡轮流量计的工作原理,以改善其精度通过计算流体力学的方法对100mm口径的气体涡轮流量计进行了数值模拟,给出了气体涡轮流量计的速度场压力场速度矢量场及其压损。研究了不同流量下的压损值,并通过实验进行了比较,结果表明数值仿真与实验结果基本吻合。
0引言
涡轮流量计是一种速度式流量计,近年来,已在石油、化工科研国防、计量等部门获得广泛的应用。涡轮流量计具有精度高、重复性好、压损小量程比大等优点,缺点是易受流体物性.的影响。
21世纪以来,由于计算流体动力学的发展,许多专业人员1-31尝试进行与流量计的内部流动.相关情况的数值仿真研究,也有一些专业人员对带有旋转机械的流场进行数值模拟,其中有几位人员9.13)]开始对气体涡轮流量计的内部流场进行数值模拟,以便优化气体涡轮流量计的内部结构。对用于天然气计量的涡轮流量计进行数学建模并做数值模拟,将其结果与流量计的实际校正曲线进行比较。采用标准k-ε湍流模型对切线型涡轮流量计进行了数值仿真。由于气体涡轮流量计是一种精度高的流量仪表,需要对内部流场结构进行正确的描述。采用精细的网格先进的方法和合理的湍流模型对气体涡轮流量计的内部流场进行数值模拟,以便优化其内部结构。
1基本控制方程
涡轮流量计的工作原理:当流体流过涡轮流量计时,在流体的作用下,叶轮受力产生旋转。叶轮的转速与管道平均流速成正比,叶轮转动后,周期性地改变磁电转换器的磁阻值,检测线圈中的磁通随之产生周期性变化和周期性的感应电势,即电脉冲信号,经放大器放大后,送至显示仪表显示。
根据动量距定理可以列出叶轮的运动方程
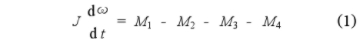
式中J一叶轮的惯性矩;dω/dt一叶轮的旋转加速度;M1一流体驱动力矩;M2一黏性阻力距;M3一轴承摩擦阻力距;M4一磁阻力距。
该文所基于的控制方程为黏性、不可压的NavierStokes方程。湍流通过Realizablek-ε模型进行封闭。程序求解框架为基于结构网格的有限体积法求解程序。连续性条件通过压力修正得到满足。动量方程湍流方程的对流项均采用二阶迎风格式离散,其他空间导数均为二阶精度的中心差分格式离散。
连续性方程与动量方程

式中μ一分子黏性系数,在引入湍流模型后,此参数可用有效黏性系数代替(μer=μt从,其中片为湍流黏性系数),
Realizablek-ε湍流模型为目前工程上使用最为广泛的湍流模型之一。采用的各种流动包括旋转均匀剪切流、包含有射流和混合流的自由流动管道内流动边界层流动和带有分离的流动等。它是两方程模型,需要求解的变量为湍动能k与湍动能耗散率ε,它们所满足的输运方程为
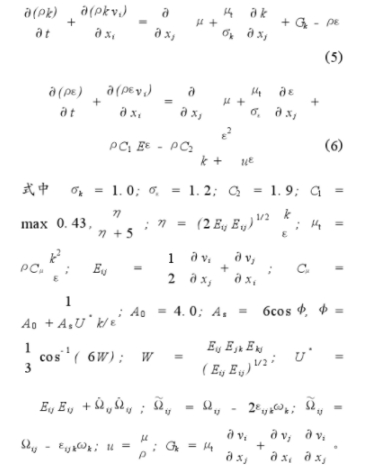
这里的Ωif是从角速度为ωk的参考系中观察.到的时均转动速率张量。
2仿真模型
研究对象为气体涡轮流量计。计算时在进出口加了十倍直径的直管段,目的是为了使其流动充分发展。计算采用的边界条件:速度为进口,压力为出口,其他均为壁面。并且采用了Fluent中的MRF模型,给定叶轮的旋转角速度来进行计算。在几何结构复杂的部位采用非结构化网格并进行了加密,目的是为了正确地显示此处的流场信息。直管段部分采用了结构化网格,目的是为了减少网格的数量,最后计算总网格达200万之多。
3仿真结果及分析
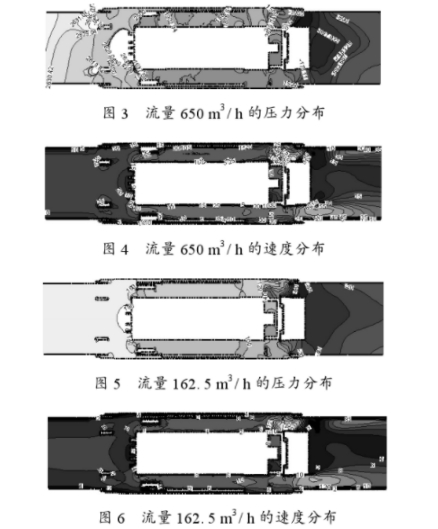
该次数值模拟流量为650,260,162.5,32m/h的情况,以下选取其中两种情况进行分析。如图3和图4所示,为流量650m³/h时的z平面上的压力(Pa)和速度(m/s)分布图。从图3可以明显看出涡轮流量计的压力损失主要集中在前后导流器和叶轮部分,而在其他部位的压力损失很小;速度分布图也很好地反映出涡轮流量计内部的流动情况。从流量.162.5m³/h时的压力(Pa)和速度(m/s)分布图,如图5-6所示,可以得到相同的结论,两种流量下,压力和速度是相似的,但大小有所不同。
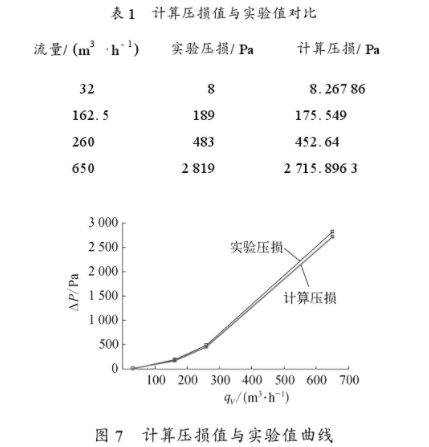
为了与涡轮流量计的实验压损值进行比较,按照实验值的测量条件,对实验值和计算值进行比.较,见表1所列和图7所示,在最大流量点上,压损计算值与实验值之差小于4%。
4结束语
该文应用计算流体力学的方法研究了气体涡轮流量计的内部流场,得到了不同流量值下的压力损失,并与实验结果进行比较,发现两者吻合很好。通过研究知道,目前的计算方法是合理的,得到的结果是可靠的,通过改变结构参数进行计算可以优化气体涡轮流量计内部结构。
本文来源于网络,如有侵权联系即删除!