摘要:电磁流量计在工农业及民生领域的流量计量中应用广泛,而电磁流量计的精度主要依靠自身的测量精度而不易受介质影响。使用多电极电磁流量计,旨在从流量计的多电极电势差角度出发提精度。基于电磁感应原理与权函数理论,提出一种改进的截面划分方法,通过COMSOLMultiphysics进行仿真,得出电极间的电势差。使用吉洪诺夫正则算法对速度矩阵进行求解,得出速度重构值。仿真与计算结果表明,该设计合理正确,仿真得到的感应电动势在截面处的速度分布符合理论分析,速度的理论值与重构值的误差不高于1.50%,显著提高了电磁流量计测量的鲁棒性与精度。
流体在管道内的流动工况普遍存在于冶金、能源和化工等众多领域,流速的测量作为工况中的一个重要指标,其精度对生产过程中流量的测量以及控制与优化都具有重要的实际意义”。
电磁流量计依据法拉第电磁感应定律制成,由于其内部没有阻碍流体流动的扰动件,而且测得的速度值与流体自身的物理参数无关,故广泛应用于化工、医药工业以及各种强腐蚀性、易爆易燃浆液的流量测量日。例如,在负担供水任务的水库管理中统计每天的放水量是一件非常重要的工作田,传统的单对电极计量被普遍用于测量导电流体的流量。国内采用--对电极的高精度中小管径的电磁流量计的精度级别达到0.2。然而,它只适用于中小管径且轴对称流的情况,在非轴对称流或者非满管情况下,其测量误差较大。实际情况中,只有当被测管道足够长时(为5~10D,D为截面直径),管道流型才会发展为充分发展流,当流速较快时,管道内流型是不稳定的,在管道上部会有波浪产生,无法通过单对电极测出正确的流速。而多电极计量可从不同电极对获得多组电势差,故可以提高非满管与非轴对称流量的测量精度用。
自1962年Shereliff给出两电极权重函数的表达式以来,随着科学技术的发展,多电极技术取到了长足的进步。然而其实现过程中存在--定困难,主要原因是划分区域过小、矩阵计算时间过长、制作成本和难度较高。国内尚不能提供拥有自主知识产权的产品。本文设计了一种8电极电磁流量计,并提出了一种改进的区域划分方法,运用COMSOLMultiphysics进行有限元仿真得出电势差,由于权函数理论公式针对8电极电磁流量计没有精确解,故采取吉洪诺夫正则化方法,通过Matlab实现流场速度分布的不适定重构求解。
本文在前人研究的基础.上,对电极数量与区域划分重新改进,旨在降低速度的重构值误差。与更多数量电极相比,该方法复杂度较低,在保证系统实时性较好的前提下,在非对称流、非满管的情况下仍可维持较高精度。
1多电极电磁流量计设计
1.1多电极流量计测量的理论基础
在对电磁计量求解Maxwell方程组时,需要设定.电势U在流量计界限处的前提条件:管道内充满介质;管道与外部绝缘,即管道壁上不存在法向电流。在实际测量中,假设磁感应强度B仅在x轴方向分布即B=Bx,流体介质按轴向流动υ=υx。因此在忽略湍流的情形下,电极A与电极B之间的电势差UAB;可表示为
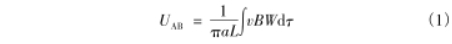
式中,α为管道内壁半径;L为电极对的直线距离;υ为流体速度;W为权重函数,只与电磁流量计结构相关;积分域T实际指所有流动的流体,因为其他方向。上速度为0,对积分没有贡献。
对于多电极电磁流量计而言,电极位置按一定的规律遍布在管道内壁,测得的感生电势有多组。如果将电极所在处的整个管道横截面划分成尺寸极小的N个测量区域,假设沿管壁布置i对测量电极,当介质流过横截面时,每对电极都得到一弦端电压U,管道切面处第n个区域对第i对电极上得到的电势权重值记作Wn.t,则式(1)可变换为
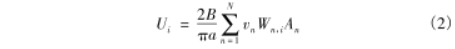
式中,N为切面所划分的区域个数;α为管道内壁半径;B为切面处的平均磁感应强度;υn为第n个区域内的轴向平均速度;An为该区域的面积大小:Wn.i为第n个区域对第j对电极间获取的感应电动势的权重函数;Ui为第i对电极间的电势测量值。
1.2电极设计与区域的划分
在使用多电极电磁流量计进行流量检测时,电极数目的选择至关重要。数目增多可提高测量精度,但是制作成本与制作难度会大幅提高,计算时间也会不可避免地增加,而若数目太少,数据精度较低,意义不大。故本文采用了一种8电极电磁流量计,旨在提高测量精度的同时保证时效性与成本。
针对8电极电磁流量计采用了一种平行布置区域的方式,在8对电极的情况下划分出3个区域,每个区域内相对应的电极处于该区域的中心位置。然而,这种划分方法只能得出同一水平高度的平均流速,无法在垂直于洛伦兹力的方向进行更精细的划分,分辨率较低。因此一种分辨率更高的划分方法。将8个电极间隔45°安装在被测截面内壁上,电极分布如图1所示,e1~e8依次表示8个电极。以电极为界限,进行竖直方向的划分,相应地会得到7个感应电势差,对应有7个求解区域’。如图1所示,从上往下将测量区域依次分成A1~A7。其中面积比较大的A.区域是被测对象横截面积最大的区域,也是产生电势差最大的区域,其他区域的面积相对来说比较小,只是A4区域面积的1/10左右。这样可以在细化划分区域的同时,保证时间复杂度不会过高,充分利用圆简管道的特点。这种划分方式可以让管道内壁的电极最大程度地读取电势值,通过区域权函数理论可以更详细地反映流场内的速度信息,提高仿真的精度。
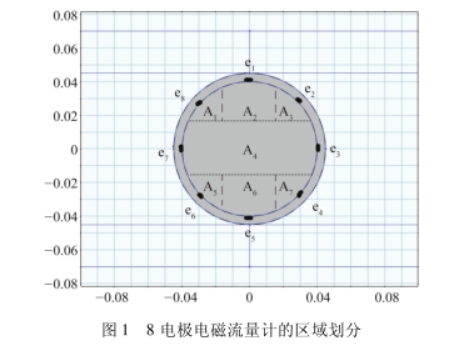
根据式(2)的表达内容,电极对间的感生电势测量值为速度与权重函数和面积的乘积求和,因此,多电极电磁流量计测量公式可改写成矩阵乘积的形式:
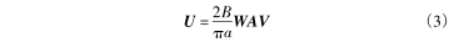
式中,W为ixj维度的区域权函数矩阵;V为包含i个区域轴向平均速度的速度向量;U为包含j个感应电动势测量值的电压向量:A为ixi维以i个区域的面积为对角元素的对角阵。在本文的应用中,i=j=7。
在实际应用中,测得感应电动势后,多电极电磁流量计在对速度进行重构以及得出流量的过程,从数学角度看其本质是一个矩阵运算的过程。
矩阵A在完成区域划分后,其面积大小为定值;并且电极所在坐标处的感应电动势可通过电极对测量出来,为因变量,因此矩阵U也已知;而区域权函数矩阵W是只与电磁流量计结构有关的常数矩阵,通过COMSOLMultiphysics仿真可求得。
2基于有限元仿真的速度重构
2.1区域电势的有限元仿真
为获得实验所用电磁流量计的权函数,首先根据实验所用的流量计结构进行仿真。
为了获取横截面电极上的仿真电势值,可在模型开发器中选择域点探针,并更新结果,即可在工作区探针表得到感应电势。在8个电极中把e1作为参考电.极,与其他7个电极构成了7对电极组合,可以得到7x7共49个电压测量值,如表1所示。
为提高权函数精度,管道内流体速度可以适当提高,分别在区域A1~区域A7沿管道方向施加速度(洛伦兹项)500m/s,经计算得到图2所示的7张电势分布图,从左到右、上到下依次是区域A1~A7域A7,施加速度的电势。.
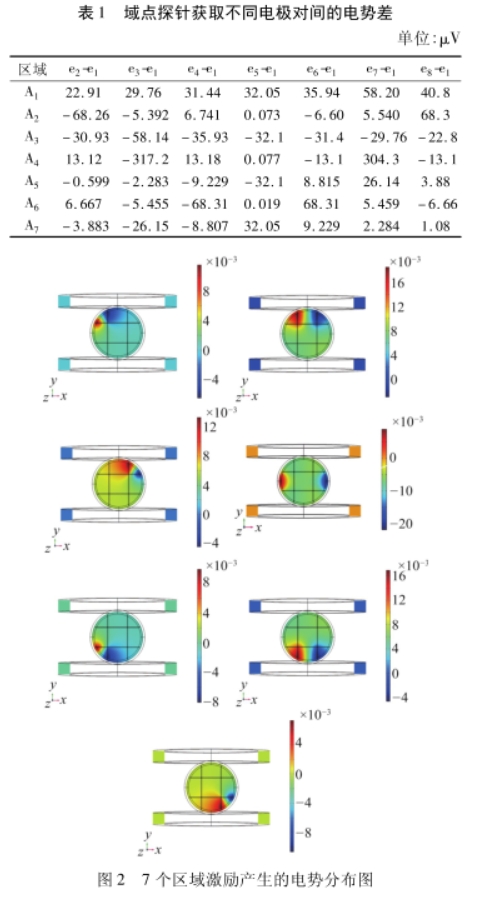
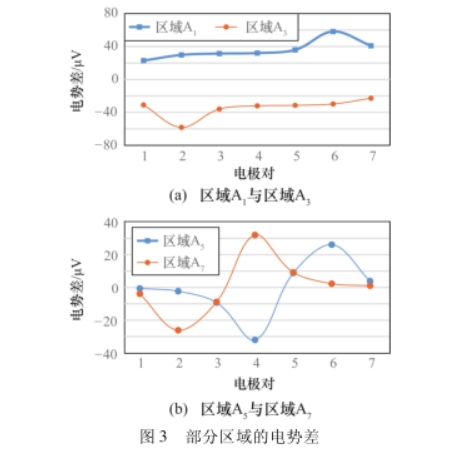
其中,部分区域的感应电势差的仿真如图3所示,从图3中的数据分布可以看出,由于仿真过程中所添加的速度分布的设置,仿真得到感应电压数据是以第
4对电极为对称中心,同时区域划分在测量面内的分布也是对称的。
通过传感器得到感应电势差后,根据式(4)进行速度的重构:
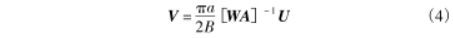
得出一维速度矩阵后,将区域速度乘以对应区域面积即可得出流量信息。
2.2逆矩阵的求解
在经典的数学物理学方程求定解问题中,问题的定解分为两类,一类是适定问题,该类问题具有以下3个特性:①解是存在的;②解是唯--的;③解连续依
赖于初始值条件。而上述3个条件只要有一个不满足就称为不适定问题。
由于多电极电磁流量计中存在极化干扰、微分干扰等误差,矩阵数据精度有限。如果采用对矩阵的精度要求较高的直接求逆法求逆矩阵,干扰与微小误差会对速度结果造成较大的影响,所以使用直接求逆法得到的逆矩阵并不精确。
为了求得具有一定精度的稳定近似解,数学物理.学中已经提出许多有效的解法,其中一种就是正则化方法。其原理是通过对原不适定问题中的算子添加一个合适的扰动项,使之稳定,从而解决逆问题的不适定性,使得产生的解是存在的[I@]。因此,采用选取吉洪诺夫正则化运算法则。在Matlab中,首先使用内置的奇异值分解函数csvd获得待求线性方程组的参数的奇异值[u,s,o];然后使用L曲线法l_curve(u,s,B)求得正则化参数lambda,最后使用吉洪诺夫正则化求解速度。求得的速度重构值如图4所示。
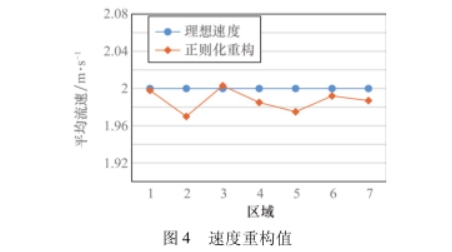
在设置为均匀流速的情况下,对感应电势差仿真数据进行正则化计算后的流速分布如图4所示,从图4中可以看出,仿真求得的速度重构值精度较高,误差在1.50%以内。
3结束语
本文基于电磁感应原理与权函数理论,为电磁传感器设计了一种8电极的多电极电磁流量计。在COMSOLMultiphysics软件.上完成了励磁线圈、圆简形管道、洛伦兹力的设计与仿真,并使用Matlab软件对速度重构矩阵进行求解。结果证明:7块区域的划分与正则化求解保证了系统在环境变化时的鲁棒性与正确率。重构后的速度与理想速度的精度在±1.50%,可以较好地实现圆简形电磁流量计的速度复原。
本文来源于网络,如有侵权联系即删除!



