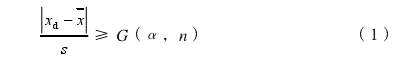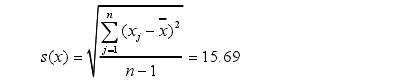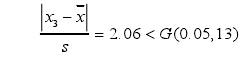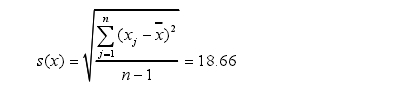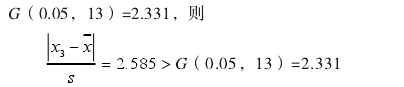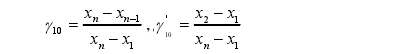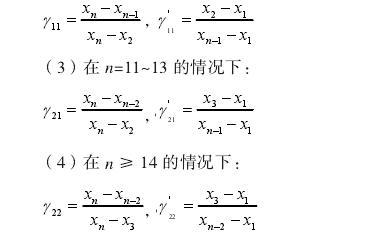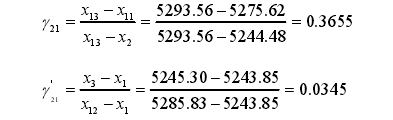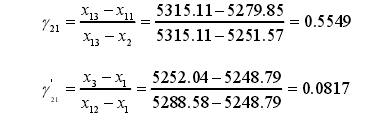随着天然气计量技术的发展和对天然气贸易交接计量要求的提高,流量计的正确计量显得至关重要。在此背景下,某省组织开展了全省气体涡轮流量计计量比对工作,以确保全省量值统一、正确、可靠,促进计量技术机构能力提升。
比对选用了一台DN150mm气体涡轮流量计作为传递标准,流量范围为(80~1600)m³/h,精度等级为1.0级。其中0.4qmax=640m³/h、.0.7qmax=1120m³/h为比对流量点,每点检测6次,测得其仪表系数K,取6次平均值作为比对值。
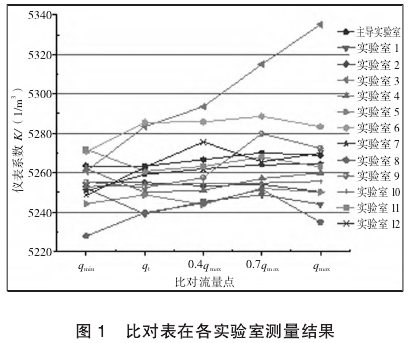
本次比对,各参比实验室完成率为100%,比对完成后,主导实验室对各参比实验室的数据进行了汇总统计,各实验室测量结果如图1所示。由图1可以看出,实验室3的测量结果随着流量增大而增大,与其他参比实验室的测量结果产生了较大偏移,需进行异常值判别。
一、异常值判别常用的统计方法
判别测量结果异常值常用的统计方法有拉依达.准则(3σ准则)、格拉布斯准则、狄克逊准则等。-般来说,在重复观测次数n>50的前提下,可以考虑使用3σ准则,但在GB/T4883-2008《数据的统计处理和解释正态样本离群值的判断和处理》中已不采用此方法;在3<n<50的情况下,格拉布斯准则效果较好,适用于单个异常值;有多于一个异常值时,选用狄克逊准则较好。
二、气体涡轮流量计计量比对数据中异常值判别
在此次气体涡轮流量计计量比对工作过程中,异常值需要慎重处理。为避免异常值的遗漏和测量真值的误判,可以综合运用多种判定方法处理异常值。考虑比对工作的重要性,此次异常值判别选用格拉布斯准则和狄克逊准则同时进行,选.用格拉布斯准则判别异常值,并用狄克逊准则判别以作验证。
1.格拉布斯准则
设在一组重复观测值xi中,其残差vi的绝对值lvil最大者为可疑值xd,在给定的包含概率为p=0.95或p=0.99,也就是显著性水平为α=1-p=0.01或0.05时,如果满足式(1),可以判定xa为异常值。
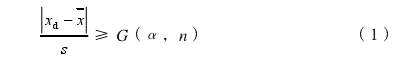
式中:G(α,n)一与显著性水平α和重复观测次数n有关的格拉布斯临界值,查格拉布斯准则临界值G(α,n)表可得;s一测量结果的实验标准偏差。
本次计算中,测量结果平均值`x和实验标准偏差s以算术平均值计算,步骤如下:
(1)0.4qmx流量点
计算过程如表1所示。参比实验室`x值的算术平均值为x=5261.28。
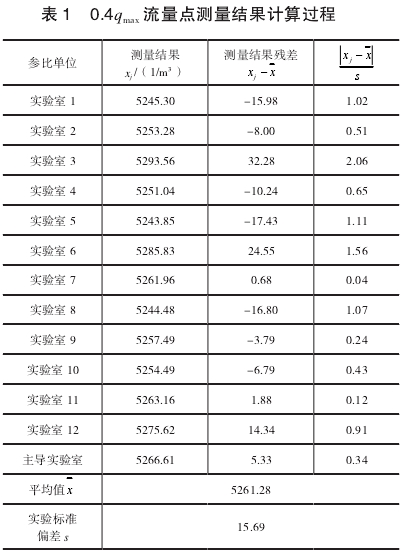
实验标准偏差为
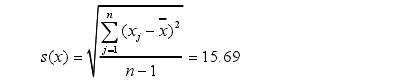
计算各个测量结果的残差xj-`x,其中绝对值最大的残差为32.28,相应的测量结果可疑值为x3=5293.6。按置信水平P=95%=0.95,即α=1-0.95=0.05,n=13,查格拉布斯准则的临界值表得到G(0.05,13)=2.331,则
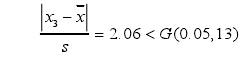
可以判定实验室3在0.4qmax.流量点的测量结果不属于异常值,不需要剔除。
(2)0.7qms流量点.
计算过程如表2所示。参比实验室K值的算术平均值为`x=5266.87。
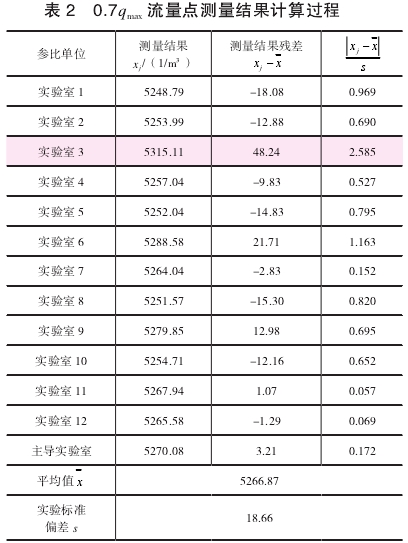
实验标准偏差为
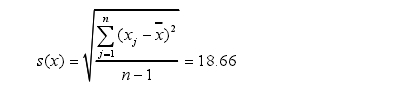
计算各个测量结果的残差,其中绝对值最大的残差为48.24,相应的测量结果可疑值为X3=5315.11。按置信水平P=95%=0.95,即α=1-0.95=0.05,n=13,查格拉布斯准则的临界值表得到
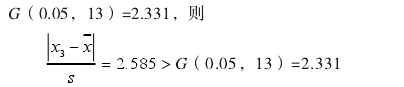
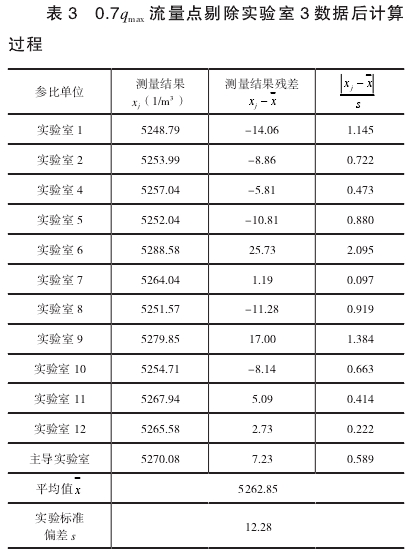
可以判定实验室3在0.7qmax流量点的测量结果属于异常值,需要剔除。剔除后,12组数据重复上述过程,计算结果如表3所示,置信水平P=95%,即α=1-0.95=0.05,n=12,查格拉布斯准则的临界值表得到G(0.05,12)=2.285,可以判断无异常值。
2.狄克逊准则验证
设,所得的重复观测值按由小到大的顺序排列为X1,X2.....,xn。按以下4种情况计算统计量γij,或γij'
(1)在n=3~7的情况下:
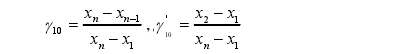
(2)在n=8~10的情况下:
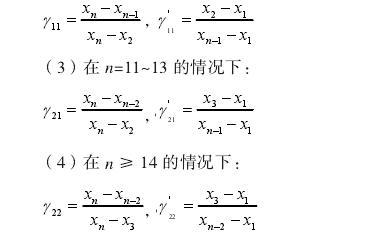
判断异常值的狄克逊准则为
若γij>γij',ry>D(α,),则xn为异常值。
若γij>γij',ry>D(α,),则x1为异常值。
式中:D(α,n)一狄克逊临界值,查狄克逊检验的临界值D(α,n)表可得。
本次计算的具体步骤如下:
测量次数n=13,将各实验室测量结果按从小到大的顺序排列为x1,x2,....X13。按置信水平P=95%,即α=1-0.95=0.05,n=13,查狄克逊准则的临界值表得到G(0.05,13)=0.557。
在n=11~13的情况下:
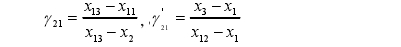
若γ21>γ21',γ21>D(α,n),则xn为异常值。
若γ21>γ21',γ21>D(α,n),则x1为异常值。
否则没有异常值。
(1)0.4qmax流量点
0.4qmax.流量点的测量结果如表4所示。
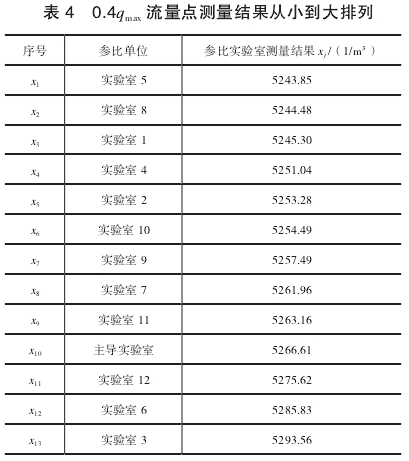
由于是属于n=11~13的情况,所以统计量计算如下
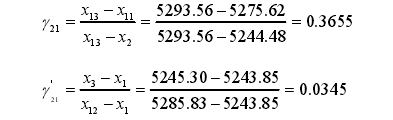
γ21>γ21',则
γ21=0.3655<D(0.0513)=0.557
可以判定实验室3在0.4qmax流量点的测量结果X13=5293.56不属于异常值,不需要剔除。
(2)0.7qmax流量点
0.7qmax流量点的测量结果如表5所示
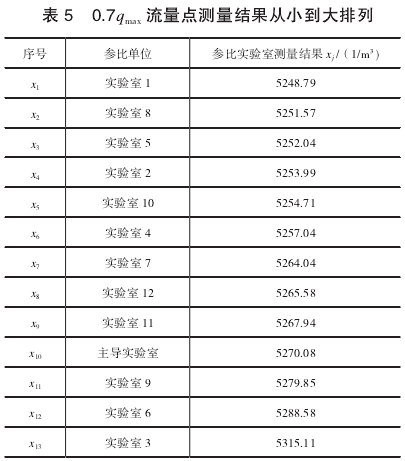
由于是属于n=11~13的情况,所以统计量计算如下
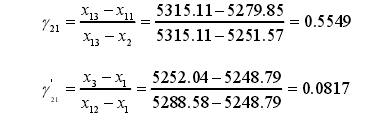
γ2>γ21',则
γ21=0.5549<D(0.05,13)=0.557
可以判定实验室3在0.7.流量点的测量结果X13=5315.11不属于异常值,不需要剔除。
三、异常值判别结果分析
综上,考虑比对工作的严谨性,在此次异常值判别时,选用格拉布斯准则和狄克逊准则综合进行。通过异常值判别结果分析可知:在0.4qmax流量点,实验室3的测量结果经过两种判别准则判断均不属于异常值,可正常参与计算;在0.7max.流量点,实验室3的测量结果用格拉布斯准则判别属于异常值,用狄克逊准则判别不属于异常值,两种判别方法结论出现矛盾。比对工作对统计数值要求较高,出现既可能是异常值又可能不是异常值的情况时,考虑将此次测量结果作为异常值考虑。最终将0.7qmax流量点实验室3的测量结果作为异常值,予以剔除。
四、结束语.
对于异常值判别方法的选择,很多学者做了大量研究,但大多集中在研究如何利用工具辅助快速正确地识别异常值,以节省时间提高工作效率。目前对于判别方法的选择还没有定论,达成比较-.致的意见是在涉及数据要求较高的场合,可以综合运用多种判别方法进行异常值判别。在实际工作中,计量检定人员除了提升工作技能,尽量避免人为因素掺人异常值以外,更要熟悉并掌握多种异常值判别方法,以保证日常检定工作中数据的有效性.和科学性。
本文来源于网络,如有侵权联系即删除!