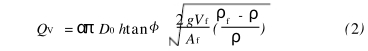摘要:浮子流量传感器中存在的非线性问题是影响浮子流量计测量精度的一个重要因素,为了解决这个问题,浮子流量传感器的特性,利用最小二乘法拟合数据,分析浮子高度和流量之间的非线性关系理论和实验研究结果表明,针对目前应用的短管型浮子流量计流量和浮子高度之间存在明显的非线性关系,并且发现在其他条件相同的情况下浮子行程的增加即锥管锥角的减小对浮子流量传感器线性度的改善具有重要的作用.
浮子流量计又名转子流量计或面积流量计.在测量过程中,始终保持节流件前后的压差不变,通过改变流通面积来改变流量,,所以浮子流量计也叫恒压降变截面流量计.浮子流量计的量程比一般可达10:1,精度约为±(1~2)%.由于浮子流量计具有结构简单、使用方便、直观、压损小、成本低等特点,已被广泛应用于实验室及生产领域".浮子流量计在测量过程中流量和浮子高度之间存在非线性关系,影响了测量精度和浮子流量计的性能,这个问题在目前广泛应用的短管型浮子流量计中尤为明显,必须寻求有效的方法来解决.
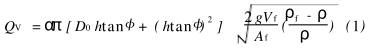
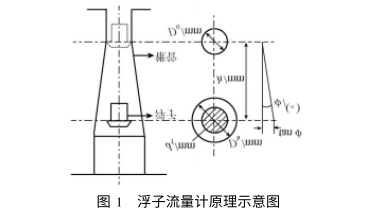
Qv为浮子流量计的体积流量,α为流量系数;h为浮子在锥管中的垂直位置;为锥形管锥半角;Vf为浮子体积;ρf为浮子材料密度ρ为流体密度;Af为浮子垂直于流向的最大截面积;D0为浮子最大迎流面的直径;Dh为浮子平衡在h高度时锥形管的直径;df为浮子最大直径(见图1).
公式(1)是习用的浮子流量计流量计量公式,一般认为在锥半角中足够小的情况下可以忽略二次项(htanφ),公式(1)可写为如下形式:
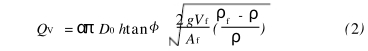
公式(2)中Vf、Af、ρf、ρ、α、q、D0及φ都是确定数值,故公式(2)中流量Qv与浮子行程h具有线性关系.
1.2研究对象
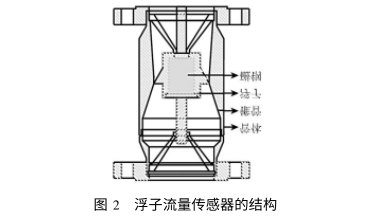
目前流行的短管型浮子流量计其高度统一为:250mm,为了和其他部件相配合,浮子在管体内能移动的最大位移为59mm,在本文中选择浮子行程分别为45mm(锥半角φ=21°06'),50mm(锥半角φ=18°16')和55mm(锥半角φ=15°15')的DN80金属管浮子流量传感器进行线性度的研究,其流量测量范围为4~40m'/h,测量介质为水,对应流量下限时的最低雷诺数为14685.浮子流量传感器的结构如图2所示.
1.3非线性误差计算公式
随着现代技术的发展,进行测量的非线性计算已非难事.目前,国内外金属管浮子流量计采用的线性化技术主要有两种:-是应用四连杆进行非线性修正;二是利用凸轮进行非线性修正.另外,还出现了带微处理器的智能流量计,采用物位传感器检测浮子位移,由微处理器通过软件进行线性化,从而使仪表结构更简化,精度更高'".故当前流行的金属管浮子流量计一般均采用250mm的仪表总长度,如图2所示,不仅可以节约原材料,加工制造简单,而且体积小,重量轻,安装使用方便.但是为了达到更好的流量测量效果,还是应该采用尽可能长的锥管,增加浮子的行程,使仪表一次测量的非线性尽可能减小
计算仪表一次测量的非线性误差时利用最小二乘法来拟合直线,非线性误差γ计算公式'"]:
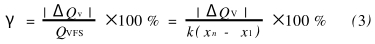
其中:△Qv为输出平均值与基准拟合直线间的偏差,QVFS为满量程输出平均值,k为拟合直线的斜率,xn为被测物理量的第n个值,x1为被测物理量的第1个值.
2浮子流量计非线性问题的理论分析
2.1理论计算数据.
为了研究浮子流量计的非线性问题,本文利用公式(1)针对浮子在锥管中的垂直位置和流量的对应关系给出了三组理论计算数据.
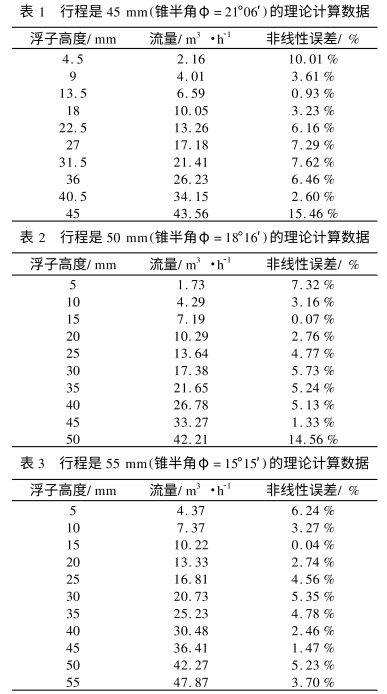
在公式(1)中,当流量传感器的结构以及被测流体介质确定下来后,φ、Vf、ρf、ρ、Af、D0、Dh、df以及α这些变量都是已知量,是不变的.表1、表2,表3分别给出了利用公式(1)计算的行程为45mm,50mm和55mm的情况下浮子高度和流量之间的对应关系,其中浮子高度是浮子在锥管中的垂直位置.数据表中的第三列是利用公式(3)计算出来的相应流量点的非线性误差.
2.2理论计算数据分析
对2.1节中的理论计算数据进行非线性误差分析.
如图3所示,(a)、(b),(c)分别是行程为45mm,50mm和55mm的浮子流量计浮子高度和流量间对应关系曲线及利用最小二乘法拟合的直线.从表1.表2,表3中第三列所示的非线性误差数据可以看出,当利用公式(1)进行流量计算时在不同的流量点处流量和浮子高度之间表现出了不同的非线性误差,流量和浮子高度之间不是线性对应关系.
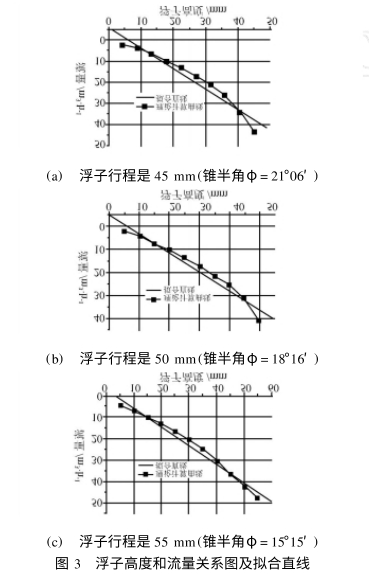
当浮子行程是45mm(锥半角φ=21°06')时:最大非线性误差γmx=15.46%,平均非线性误差γ=6.34%
当浮子行程是50mm(锥半角中=18°16')时:最大非线性误差Ymax=14.56%,平均非线性误差γ=5.01%.
当浮子行程是55mm(锥半角φ=15°15')时:最大非线性误差Ymax=6.24%,平均非线性误差γ=3.61%.
对比三个不同行程下最大非线性误差和平均非线性误差的数值可以看出,当浮子行程分别为45mm.50mm,55mm,即相应的锥半角为φ=21°06'φ=18°16'中=15°15'时,无论是非线性误差的最大值还是平均值都有很明显的减小,尤其是浮子流量计的线性度即最大非线性误差分别为γmax=15.46%、γ=14.56%,γmax=6.24%,浮子流量计的线性度从理论计算上有了明显的改善.
3浮子流量计非线性问题的实验研究
该过程对如1.2节所述的浮子流量传感器进行实验研究.
3.1实验装置
实验装置如图4所示,采用称重法对金属浮子流量计进行标定.实验过程如下所述:
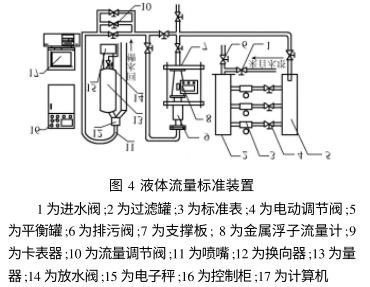
实验中所需流体介质来自高位稳压水塔,流体经过进水阀1进入过滤罐2,3为标准表,可以监视管道中的流量值,电动调节阀4起选通作用,从平衡罐5流出的流体进入金属管浮子流量计8,再经过流量调节阀10从喷嘴11不断向量器13中注入,当量器13中注满流体以后换向器12自动换向,使得从喷嘴11流过来的流体不再进入量器13,而是进入量器13右侧的回水槽,此时电子秤15可以称出量器13中流体的重量,通过计算机17中的程序显示结果可以看到流量值,之后打开放水阀14放水,当量器13中的水全部都放完时,电子秤15清零,换向器12又自动换向到量器13-侧,使得流体不断的注入,准备下一次实验.
3.2实验数据
实验过程中选取10个流量点进行实验,单行程每点重复测量3次,正反行程各5次.对每个实验点处的样本取平均(30次平均值).实验数据如表4,表5和表6所示,其中标准流量是实验过程中利用称重法得到的流量,即流过金属浮子流量计的流量,浮子高度是浮子在锥管中的垂直位置.同样数据表中的第三列是利用公式(3)计算出来的非线性误差.
3.3实验数据分析
如图5所示为根据实验过程中所得到的标准流量和浮子高度之间的对应关系曲线及相应的利用最小二乘法得到的拟合直线.
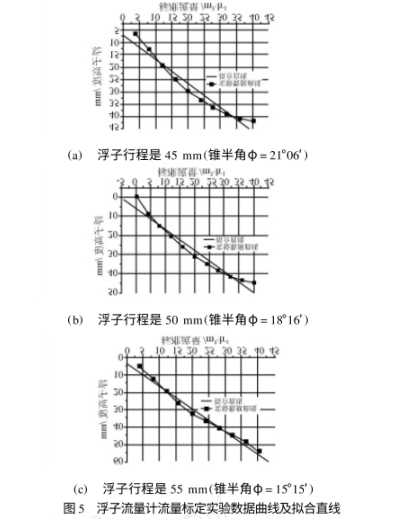
下面对行程分别是45mm、50mm,55mm的浮子流量计的非线性误差值作一下比较.从表4、表5,表6中的非线性误差数据可以看出,在实验过程中流量和浮子高度之间也并不是简单的一对应的线性关系,二者之间存在严重的非线性,这也进一步证明了在进行流量计算时不能利用公式(2)对流量和高度之间的关系进行线性化处理,而应该利用公式(1)进行计算.
当浮子行程是45mm(锥半角φ=21°06')时:最大非线性误差γmax=12.43%,平均非线性误差γ=6.71%.
当浮子行程是50mm(锥半角中=18°16')时:最大非线性误差γmax=11.45%,平均非线性误差γ=5.08%.
当浮子行程是55mm(锥半角φ=15°15')时:最大非线性误差γmx=5.66%,平均非线性误差V=3.28%.
对比.上述两组最大非线性误差和平均非线性误差的数值可以看出,当浮子行程为45mm、50mm,55mm,相应的锥半角为φ=21°06'φ=18°16'φ=15°15'时浮子流量计非线性误差的最大值和平均值也都有了很明显的减小,其中浮子流量计的线性度即最大非线性误差分别为γmax=12.43%γmax=11.45%γmax=5.66%,仪表的线性度得到了很好的.改善.
4结论
本文针对浮子流量计的线性度问题进行了研究,文中给出了在三种行程下不同的流量点处的非线性误差值,并从理论和实验做了对比分析.理论分析和实验研究表明,在目前应用的短管型浮子流量计中流量和浮子高度之间不是一--对应的线性关系,因此在进行流量计时不能选用公式(2),而应该选择公式(1).
分析两个行程下的浮子流量计非线性误差数据可以得到如下结论:浮子的行程(锥管的锥角)是影响浮子流量计线性度的一个重要因素,适当增加浮子的行程、减小锥管的锥角,可以使一次仪表的线性度有很大的改善,这对于浮子流量传感器结构的设计与优化具有重要的指导意义.
本文来源于网络,如有侵权联系即删除!