摘要:F双钝体旋涡脱离的流体动力学特性以及利用双钝体增强流体振动的最佳组合结构。给出了多种钝体组合结构的斯特劳哈尔数的试验结果,表明双钝体结构具有常定的斯特劳哈尔数。用50mm口径涡街流量计进行的试验证明,双钝体组合在一定的条件下能获得理想的旋涡重叠,从而增强流体的振动。在钝体的轴对称点上,还观察到强度和频率相同,相位相差180°的流体振动点,利用优化的双钝体结构和差动传感技术,研制出小流量灵敏度和抗干扰性能很好的新型旋涡流量计。
0前言
斯特劳哈尔和冯·卡门对钝体绕流所做的开拓性研究揭示了旋涡脱离的基本特征和规律,即:当流体流经钝体时,尾流中将形成旋涡流型,旋涡从钝体两侧交替地脱离,并在---个较宽的雷诺数范围内,有常定的量纲一的脱落频率,即斯特劳哈尔为常数。这表明旋涡脱落的频率与平均流速成正比。
Roshkol21的研究给出了更为明确的结果,即在雷诺数处于300<Re<2X105的范围内时,斯特劳哈尔数保持在0.2左右,他还首次提出了利用斯特劳哈尔数的常定范围来制造流量计的设想。20世纪70年代初,商品化的涡街流量计在日本出现。近30年的工业应用证明了涡街流量计在稳定流体计量中的可靠性和精确性,它的主要优点还包括精度高、线性度好、介质适应性宽和性能可靠(无运动部件)3]。然而,涡街流量计存在的流量下限高和抗干扰性能差等问题,使它丧失了许多潜在的应用领域,如:量大面广的天然气商业计量以及流速和压力不稳定的测量系统。
为了将涡街流量计应用于不稳定流体的计量,本文利用钝体组合强化旋涡脱落诱发流体振动的理论研究基础上,设计出双钝体涡街流量计试验样机:通过试验获得了双钝体的最优组合结构及参数;分析了钝体组合对斯特劳哈尔数的影响;同时在后钝体的轴对称点上,还观察到强度和频率相同,相位相差180°的流体振动点,这些研究结果为研制具有良好抗干扰性能和小流量灵敏度的双钝体差动式涡街流量计提供了依据。
1双钝体涡街流量计的原理
双钝体涡街流量计的基本设计思路是利用前钝体和后钝体引发的旋涡脱离现象,通过试验获得使旋涡在后钝体周围实现同相位叠加的最佳钝体组合,使流体振动得到加强,降低计量的下限,同时利用钝体两侧的流体振动具有180°相位差的特点,用差动式传感器抑制共模干扰信号的方法,提高流量计的抗干扰性能,图1所示为双钝体涡街流量计的原理。
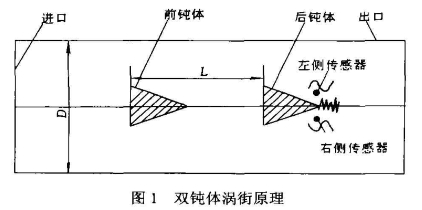
2试验装置
图2所示为试验装置及测试系统原理。
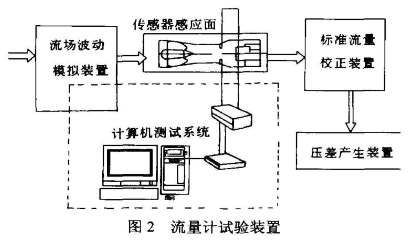
试验装置为气体流量试验系统,它由5个部分组成。I一流场波动模拟装置,用于实验室条件下模拟流场波动;II一试验表体;II一标准流量校正装置,本试验台采用临界流文丘利喷嘴流量计作为校准其他仪表的基准;IV一负压产生装置,本试验台通过真空泵产生负压,使试验台的入口和出口之间产生一个压差,这样就形成一个小型风洞。真空泵电动机额定功率为11kW,额定转速为1450r/min;V一计算机测试系统,主要由电荷放大器、DAC-TRON公司Photo便携式动态信号分析仪(该分析仪的主要特性和性能指标:4个输入通道,一个输出通道;120MHzTMS320VC33DSP,21kHz处理率;32位浮点DSP;ICP传感器供电;USB接口,支持热插拔;质量小于200g,抗振动外壳)及计算机所组成。
试验台的临界流文丘利喷嘴测定装置由5个标准的不同喷嘴流:量计组成,通过不同的组合方式可得到5.5--220.5m³/h之间的流量。试验的管道内径50mm。
3试验结果
试验分为两个部分,1一双钝体组合涡街振动频率试验;2一双钝体组合方式对涡街强度的影响。试验传感器如图1所示对称于后钝体安装。试验表体直径为50mm。
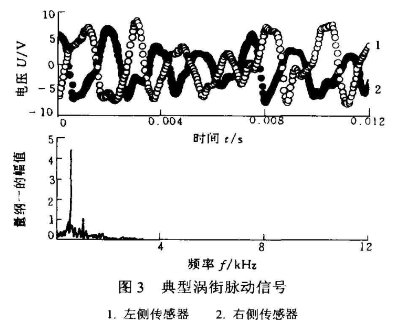
典型的涡街脉动信号如图3所示。从信号的时域信号可以看出。对称于后钝体两侧涡街的脉动是反相的,并有明显的周期性,其功率谱的频率分布很广并有一个明显的峰值,该峰值处频率和时域信号的主波动是频率是相同的。定义功率谱中该峰值处的频率为涡街的主频。下面所讨论的涡街频率指的就是涡街的主频。
3.1双钝体组合涡街振动频率试验研究
对于单钝体涡街,在临界雷诺数之上斯特劳哈尔数是恒定的,这是单钝体涡街流量计的测量基础。双钝体涡街是否存在同样的规律是双钝体涡街流量计的关键。本部分的试验研究是为寻找当旋涡发生体是两个三角形时涡街的斯特劳哈尔数是否发生变化。本部分的另一个目的是研究钝体的平行组合对涡街斯特劳哈尔数的影响。
试验所用双钝体组合图1所示,图中的前后.钝体的互相平行的,钝体的组合方式是指两个钝体之间的距离不同情况的组合。
试验的设计是对相同的钝体组合在不同的流量情况下进行试验。以得到不同组合下不同流量的测量数据。试验的采用数据如表所示。
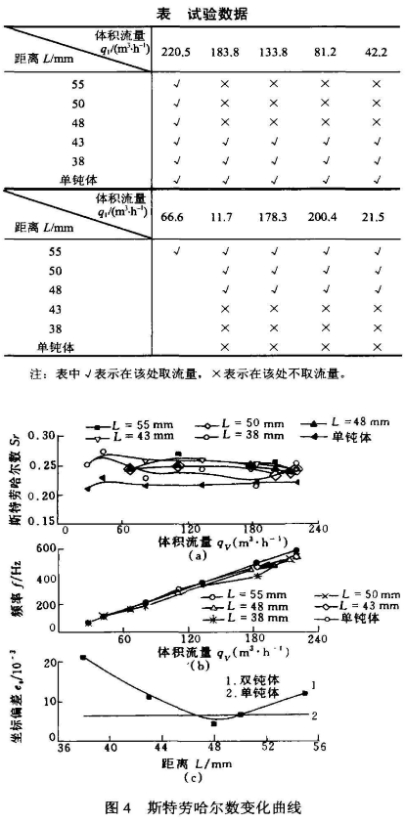
流量的选取不少于5个点,并通过流量不完全相同的选取来达到覆盖较多流量范围的目的。图4a为试验所得的各组双钝体和单钝体斯特劳哈尔数;图4b是流量和涡街频率的关系曲线:图4c为各组双钝体和单钝体斯特劳哈尔数标准偏差曲线。
从图4a和图4b中可以得出如下结论。
双钝体的斯特劳哈尔数比单钝体斯特劳哈尔数大,不同组合双钝体的斯特劳哈尔数是不相同.的。不同的双钝体组合的斯特劳哈尔数的波动不相
同的,其斯特劳哈尔数的标准偏差如图4c所示。从图4c中可以知道,双钝体的斯特劳哈尔数波动是比较大的,在L=50~46mm之间偏差与单钝体偏差相当。
由4b图,该曲线的线性度与斯特劳哈尔数标准偏差相对应,当L=50~46mm时双钝体流量--频率曲线的线性度较好。
综上所述,对于双钝体涡街流量计从测量的线性范围角度考虑应选择L=50~46mm之间的组合方式。
3.2双钝体组合方式对涡街强度的影响
上面得出双钝体流量计最佳线性范围条件。流量计的另-一个重要的问题是涡街强度,其直接影响测:量信号的信噪比。其对降低量程下限有重要的意义。
为研究双钝体组合对涡街强度的影响。设计了如下试验。试验装置如图1所示;通过改变距离L对钝体进行组合并对该组钝体在不同流量下进行试验。试验所使用的流量是220.5m3/h,178.3m'/h,111.7m3/h,66.6m3/h等4组。使用的钝体组合有L=60mm,55mm,54mm,51mm,49mm,47mm,45mm,43mm,41mm,39mm,37mm,35mm,33mm,32mm,29mm等15个组合。
进行强度比较之前,需要对涡街的信号特点进行分析并定出可以度量强度的量。如图3涡街信号是周期性的但其波动的幅值不等,故涡街的强度需要从统计.上进行比较。试验中制定的涡街强度的统计量为.

这里`y表示的是脉动压力信号平均的波动幅值,通过换算可得到涡街的平均脉动强度。以后的所有有关强度比较都是以`y为的度量。
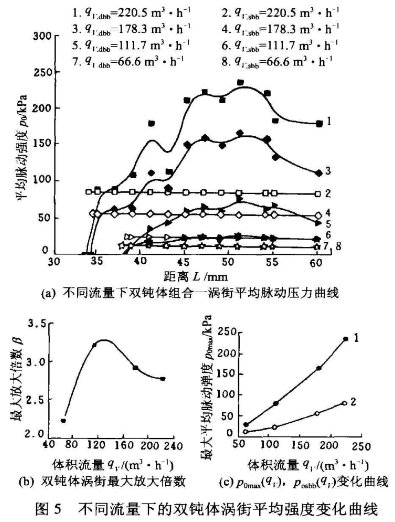
图5a是试验得到涡街的程度在不同组合在不同流量下的比较曲线,图上的P0是通过`y换算而.来的,可以认为是涡街的平均脉动强度。
图5b是不同流量下的涡街平均脉动强度最大的放大倍数,这时定义

从不同组合在不同流量涡街强度比较曲线可以得到以下结论:
双钝体对涡街的强度有加强的作用。在不同的流量下双钝体对涡街的加强程度是不一样的如图6a所示。从qv---β可以知道在不同流量下涡街平均强度最大的放大倍数是不相同的,β在qv=130m3/h时达到最大。
P0随L非线性变化,在L=45~54mm之间P0梯度很小,即在该区域内L的变化对涡街强度的影响不显著。
涡街的强度有一个峰值区域。当偏离这个区域后涡街的强度发生明显的衰减。该峰值区域与较小P0梯度区域重合。
相同流量下,双钝体涡街强度始终比单钝体涡街大。在流量不变情况下,当双钝体涡街强度接近单钝体涡街强度时,微小的L变化会导致双钝体卡门涡街现象的消失,即存在一个产生双钝体卡门涡街的临界距离Le,且Le与流量有关,在Le处双钝体涡街强度和单钝体涡街强度相等。当L<Le该流量下双钝体卡]涡街现象将消失。但Le是否与尺度相关需要进一-步的研究。同样随L不断增长是否也存在一个临界距离也需要进一步研究。
4结论
通过上述的试验研究,可以得出以下的结论:用双钝体诱发卡门涡街可以增强涡街的脉动平均强度,有利于提高测量的信噪比,降低涡街流量计的测量下限。最大强度钝体的组合L=45~-54mm。
通过适当的选择钝体的组合,双钝体涡街流量计的精度和单钝体涡街流量计是相当的。最佳线性度钝体组合为L=46~50mm。
综上述,通过两个三角型钝体组合可以得到与单钝体涡街流量计测量精度相当但信号信噪比高、测量下限较低的双钝体涡街流量计。双钝体的最佳组合方法是L=45~50mm之间。
本文来源于网络,如有侵权联系即删除!






