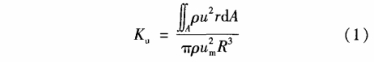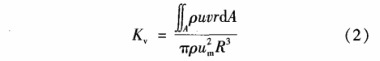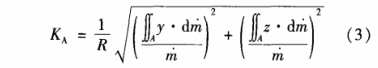摘要:利用数值计算方法研究了不同安装条件对涡轮流量计性能的影响。计算结果分析表明,安装于流量计前的单弯头、双弯头以及阀门等管道配件都会造成流体速度趋于扁平分布和不对称分布以及产生漩涡流,都是影响流量计计量精度的主要原因。合理布置弯头和阀门开度的方向,使流体通过两者时产生的漩涡流旋转方向相反,则有利于降低流量计进口前漩涡流的强度,减少对流量计测量精度的影响。涡轮流量计的前导流件能有效消除流体速度中的漩涡流分量,但在校正速度分布的不对称性和扁平性方面效果并不显著。
1引言
涡轮流量计的测量精度易受到流量计前管线安装条件的影响。一般管线系统中的各种管配件,包括阀门、弯头、变径管等所产生的流体干扰都会引起流体速度分布发生畸变,产生漩涡流和非对称流等,影响了涡轮流量计的测量精度。安装条件对涡轮流量计性能的影响早就引起各国学者的广泛关注,并对此问题进行了较为系统的实验研究。先后利用实验研究了涡轮流量计进口前装有90°弯头、不在同一平面内的双弯头、IS09951推荐的能够产生高和低流体干扰的管线结构以及阀门]等对涡轮流量计测量精度的影响。
近几年数值计算方法逐渐应用于涡轮流量计的研究中(8-12],与实验方法相比,数值计算方法具有成本低、更能提供详细的三维流场以及能掌握管线结构引起的各种流体干扰的衰减规律等优点。数值计算方法的有效性也逐渐得到了验证E[8.12].但是迄今为止仍未见文献报道利用数值计算手段研究安装条件对涡轮流量计性能的影响。
另一方面,机动油料装备逐渐向小型化发展,选用计量装置时通常考虑选用测量精度高、质量轻的流量计,如涡轮流量计。然而涡轮流量计对前后直管段的要求限制了其在机动油料装备上的使用。为此,本文利用数值计算手段就流量计进口前装有90°弯头、不在同-平面内的双弯头以及双弯头之间有一个半圆形挡板三种安装条件对流量计内部流场以及测量精度的影响进行研究,为涡轮流量计在机动油料装备上的应用提供指导。.
2流体速度分布的特征参数
流体干扰影响涡轮流量计测量精度的速度畸变主要体现在三个方面:速度分布的扁平性、漩涡流和速度分布的非对称性。为了能定量描述流体干扰引起的速度畸变,Mickan定义了轴向动量数K。、漩流数K,和非对称数K,三个特征参数5)。本文引人这三个参数,以便于后面的分析。
轴向动量数K。用于衡量流体轴向动量通量的转动力矩的大小,其计算式为:
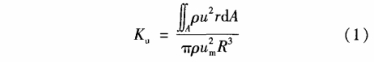
式中:u为轴向流速,um为平均流速,r为径向坐标,ρ为流体密度,R为管线半径,A为管线的横截面积。对于充分发展流,Ku为定值,约为0.62,而我们所关心的是充分发展流与干扰流之间的差别,故常用反映两者差别的参量△Ku(其值等于Ku-Ku0),它对涡轮流量计的测量精度具有较大的影响。.
漩流数Kv用于衡量轴向漩涡的强度。由于涡轮流量计的转速易受漩涡流的影响,因此Kv的大小对其有重要的影响。其计算式为:
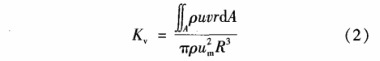
式中:v为切向流速。
非对称数KA用于衡量速度分布对称性的程度,用管线横截面上流体质心与对称轴之间的距离来表示,其计算式为:
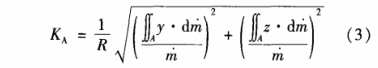
式中:y、z分别为管线横截面上的直角坐标,m为质量流量。
3数值计算模型
3.1基本方程组
描述涡轮流量计内部流场的基本方程组为连续性方程、N-S运动方程和紊流模型。目前还没有普遍适用的紊流模型,本文选用较常用的标准k-ε双方程模型。模型方程中相关系数取值分别为:Cμ=0.09,C1=1.44,C2=1.92,σk=1.0,σε=1.3。
3.2网格划分和边界条件
在数值计算过程中,涡轮流量计的叶轮处于旋转状态,故叶轮部分的网格划分疏密对计算结果的正确率具有重要的影响,在网格划分时对叶轮表面的网格进行了适当的局部加密处理。前、后导流件部分区域采用六面体网格,其他区域采用四面体网格,叶轮部分全部采用四面体网格,单流量计计算区域内网格总数为97.31万个,其中叶轮部分的网格总数为67.42万个。
为了减少在计算过程中因计算域进口与出口位置对涡轮流量计内部流场的影响,本文计算域的进口与出口适当向外作了延伸,上游直管段长度为.5D,下游为10D。进口采用圆管紊流流速分布的1/7律来确定。凡与流体相接触的所有固体界面上采用无滑移固体璧面条件,出口施加定静压。
4数值计算
4.1流量计前的管线结构
文中采用的涡轮流量计结构如图1所示。流量计的内径为15mmm,叶轮叶片数为4片,前、后导流件采用椭球形端面。
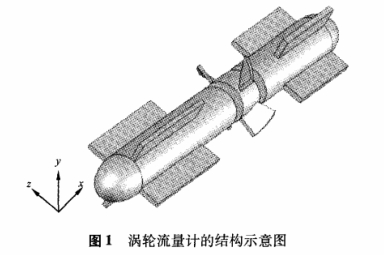
本文主要分析了Casel~Case5等5种结构,见图2。
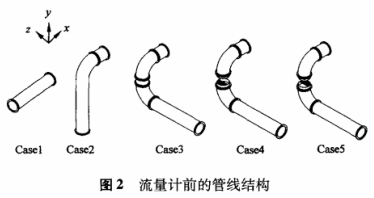
Case1:流量计前是一长为5D的直管段。
Case2:90°的弯头,其前有一5D长的直管段。考虑到机动油料装备上流量计的安装空间非常受限,弯头与流量计进口之间的距离设为1D。
Case3:不在同一平面内的双弯头,两弯头之间有一长为0.5D的直管段,进口管段长度和第二个弯头与流量计进口的距离同Case2。
Case4:在Case3的双弯头中间位置上布置了一个1mm厚的半圆薄板,薄板位于双弯头的外侧位置。
Case5:除了半圆薄板的位置在双弯头的内侧外,管线结构同Case4。
研究Case4和Case5的管线结构主要目的有两个:一是研究阀门对流量计测量精度的影响;二是阀门开度与弯头的相对方向不同时对流量计测量精度的影响。
4.2计算结果与分析
计算参数:流体的进口平均速度um为5m/s,计算介质为20℃的水。
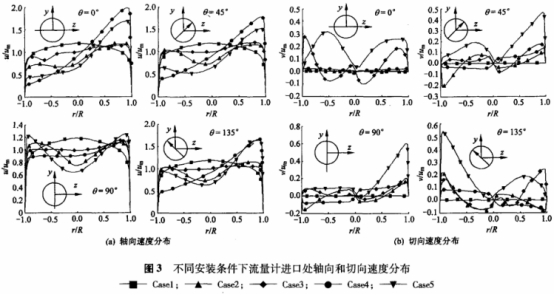
图3示出了不同条件下涡轮流量计进口处在4个方向上的轴向和切向流速分布。从图中可以看到,对于Casel这种管线结构,轴向流速符合充分发展流的速度分布,切向流速分量很小。而且在进口横截面上,根据式(1)~(3)计算得到Ku0等于0.62,Kv和KA分别等于0,因此可作为参考量用于其它管线结构的分析。本文对所有计算结果的分析都以此作为参考进行的。
当流量计前装有90°弯头时(Case2),轴向流速在管线对称轴上附近表现为最小,然后向管壁两侧增加,呈现了非对称的马鞍型分布,且切向流速表现出了二次流现象。
当流量计前的管线结构为不在同一平面内的双弯头时(Case3),轴向流速出现了与Casel相似的非对称的马鞍型分布,不过其不对称程度要比Casel小,但流速更呈扁平分布;切向流速同样出现了二次流现象,其漩涡强度则要比Casel强得多。
对于两个弯头之间有一半圆薄挡板的两种管线结构Case4和Case5,轴向流速的不对称分布非常严重。除了在θ=90°这个方向上轴向流速呈马鞍型分布外,在其余三个方向上几乎是从管璧的一.侧向另-侧单调递增的趋势。不过,两种管线结构的切向流速则表现出了不同的分布趋势。当半圆薄板布置在双弯头的外侧(Case4),流体速度中含有很强的切向流速分布,其最大值几乎达到了平均流速的60%。当半圆薄板布置在双弯头的内侧(Case5),切向流速分量要比Case4的小得多,甚至小于Case3。
造成这种差别主要是由于对于Case4,流体通过半圆薄板后产生的漩涡方向和通过弯头后产生的漩涡方向相同,因此在流量计进口前表现出比Case3更高的切向流速分量,而Case5的情况则反之。由于这个原因,Case4计算得到的涡轮流量计仪表系数与Casel相比,其误差偏移为-1.79%,而CaseS则仅为-0.23%,见表1。这个计算结果同时说明了在涡轮流量计前合理布置弯头和阀i]开度之间的相对方向,有助于降低漩涡流的强度,从而减少对流量计量性能的影响。同样我们研究了流体通过前导流件后在其轮毂末端处轴向流速和切向流速的分布情况,见图4。
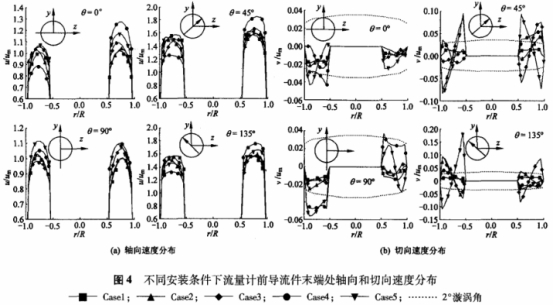
从图4中可以看到,受导流件轮毂的影响,流道面积减少,轴向流速增加;在θ=90°和θ=0°两个方向上正对导流件叶片,受其尾流的影响,轴向流速明显要比其它两个方向上的轴向流速低。从图中同时可以看到,流体经过前导流件的导流作用后,切向流速显著减小,在θ=90°和θ=0°两个方向上漩涡角的大小基本上能满足ISO9951规定的小于2°的标准,图中以虚线表示,在其它两个方向上切向流速的最大分量也不超过平均流速的20%;但是其轴向流速的不对称分布和扁平性并没有得到有效的改善,同样是Case5的轴向流速的不对称分布最为显著。
不同安装条件下在涡轮流量计进口和前导流件轮毂末端两个横截面上Ku、Kv、KA、以及流量计仪表系数误差偏移的计算值见表1。
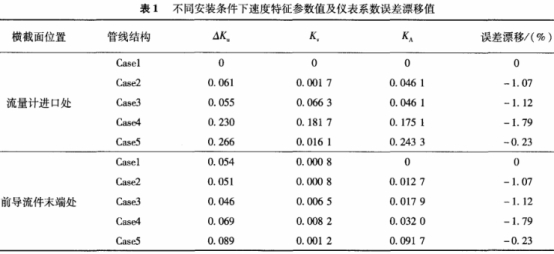
从表1中可以看到,造成流量计仪表系数误差偏移最大的是Case4这种管线结构,达到了-1.79%,这和前述分析相一致。表中的结果同时说明了涡轮流量计中的前导流件消除漩涡流的效率非常高,但是其在改善速度分布的不对称性和扁平性上的效果并不显著。因此,认为若将涡轮流量计的前导流件结构进行改进,采用孔板整流器和翼式整流器相结合的组合式结构,这样既能有效消除漩涡流,又能有效改善速度分布的不对称性和扁平性,必将显著改善导流件的整流效果,减少涡轮流量计进口流速分布对测量精度的影响,降低其安装要求,使其更适合用于机动油料装备上的计量装置。
5结论
本文利用数值计算手段研究了流量计前安装有单弯头、不在同一平面内的双弯头以及双弯头之间有一半圆挡板等管线结构对流量计内部流场和测量精度的影响,得到了以下结论:
(1)由管线结构引起的流体干扰造成流体速度分布含有漩涡流分量、轴向速度分布不对称性和扁平性,使流量计计量产生误差,本文的算例中最大误差达到了-1.79%。
(2)弯头与阀广1开度之间的相对方向影响流量计的测量精度,若流体通过弯头和阀门时所产生的漩涡流方向相同,则增加了流量计的计量误差,反之则减少计量误差。
(3)流量计中前导流件能有效减少漩涡流强度,但在改善速度分布的不对称性以及扁平性方面的效果并不明显。
本文来源于网络,如有侵权联系即删除!