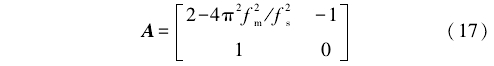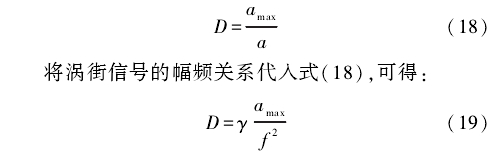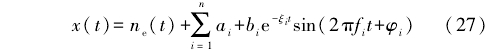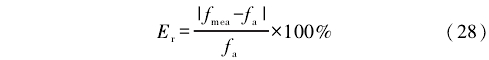摘要:为了改善涡街流量计的性能,提出了一种基于卡尔曼滤波的涡街信号处理方法。根据涡街信号的特点,设计了一个线性涡街信号模型。结合模糊搜索和迭代算法,通过分析卡尔曼滤波器算法的原理和关键参数,改进卡尔曼滤波器算法。通过仿真模拟和实际流量实验验证了所提出的方法,并与其他方法进行了比较。实验结果表明,所提出的方法具有自适应滤波、抗干扰能力和滤波速度的优点。
0引言
涡街流量计作为一种振动型流量计,具有应用范围广、测量介质多耐高温、耐高压等优点,具有广阔的发展前景。涡街流量计利用流体振动的原理来测量流量。当流体通过一个垂直放置的非流线型旋涡发生体时,发生体两侧会产生两排交错排列的旋涡,被称为卡门涡街,如图1所示。发生体后方的应力型压电传感器将旋涡产生的压力差转换为电荷信号。电荷信号的变化频率与旋涡的产生频率-致。
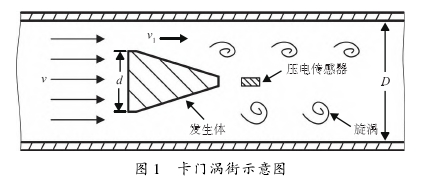
涡街信号具有以下两个特点。
1)压电传感器输出的电荷信号QH满足正弦规律,如式(1)所示
QH=γρƒ2sin(2πƒt+φa)(1)
式中:γ为压电传感器的系数,ρ为流体密度,ƒ为涡街频率,φa为初始相位。
2)在涡街流量计中,电荷放大器一般用于将传感器输出的电荷信号转换成电压信号。电压信号是待处理的原始信号,和电荷信号一样为正弦波形式。当流体密度和发生体的宽度为固定值时,涡街信号的幅值与频率的平方成正比,如式(2)所示
α∞ƒ2(2)
式中:α为涡街信号的幅值。
由于涡街流量计的传感器属于振动型传感器,很容易受到振动干扰,这对涡街流量计的测量精度和测量范围有很大的影响。由于涡街信号的幅值与频率的平方成正比,在高流速下信号的信噪比大,信号受噪声影响小;在低流速下信号的信噪比小,信号受噪声影响大,增加了信号检测的难度。国内外众多学者对这一问题进行了研究(2-3]。近年来,卡尔曼滤波方法也开始被应用在涡街流量计的信号处理中。
卡尔曼滤波是科学家R.E.Kalman等在1960年提出的一种适用于离散随机非平稳系统的最优估计算法。它基于线性离散系统,将最优滤波理论与状态空间思想相结合。宋开臣等[4]针对压电式涡街流量计抗干扰性差的缺点,提出了基于多传感器融合的涡街信号检测方法。该方法通过无迹卡尔曼滤波算法将压差传感器测量的钝体前后压差和其下游的涡街信号频率进行融合,增强了压电式涡街流量计的抗振能力,有效提高了数字带通滤波器的测量精度。Shao等[5]针对涡街流量计提出了一种基于分段卡尔曼滤波的数字信号处理方法。该方法首先分析瞬态冲击的特性,建立数学模型,然后在流量信号数据中找到含有强瞬态冲击的数据段,并对数据段进行卡尔曼滤波,以降低瞬态冲击的功率。
本文提出了一种基于涡街信号模型的卡尔曼滤波的信号处理方法(以下简称“本方法")。首先,根据微分原理和线性矩阵对非线性的涡街信号进行线性化处理并建立模型;其次,根据涡街信号的幅频关系,初始化涡街信号模型频率;再次,将滤波后的输出频率作为下一个循环的初始涡街模型频率进行迭代和模糊搜索,直到输出频率与模型频率的误差在涡街流量计允许的误差范围内为止;最后,通过仿真实验和实流实验对该方法进行了验证。
1卡尔曼滤波原理和涡街系统模型
1.1卡尔曼滤波原理
卡尔曼滤波是一种利用线性系统状态方程,通过系统输人的观测数据对系统状态进行最优估计的算法。其基本原理如下:假设有一个离散的线性系统Xk,通过k-1时刻的最优估计Xk-1得到k时刻的预测值Xk|k-1,并用k时刻的观测值Zk修正预测值,从而得到h时刻的最优估计Xk。图2显示了卡尔曼滤波原理。
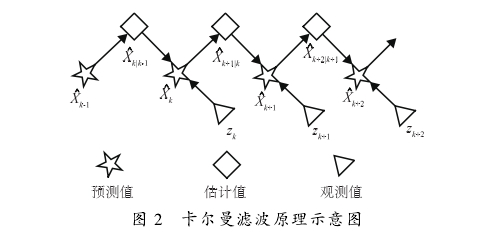
对于没有控制输人的系统,卡尔曼滤波算法的状态方程和观测方程可用式(3).式(4)表示
Xk+1=AXk+Bwk(3)
Yk+1=HXk+1+Dʋk+1(4)
式中:Xk为n维的状态变量在k时刻的值,wk为p维的过程噪声,Yk+1为m维的观测变量,ʋk+1为m维的观测噪声,A为变量Xk的状态转移矩阵,H为系统参数矩阵,B为过程噪声的系数矩阵,D为观测噪声的系数.矩阵。wk和ʋk+1是均值为0且互不相关的高斯白噪声。不难看出,由式(3)和式(4)构建的系统模型不包含涡街信号的特征。
1.2涡街系统模型
由于涡街信号是非线性正弦波信号,不满足卡尔曼滤波系统模型的线性要求,不能成为卡尔曼滤波算法的系统模型,需要利用微分原理和线性矩阵对涡旋信号进行线性化处理,具体推导过程如下。
假设,涡街信号的数学模型如式(5)所示:
s(t)=asin(2πƒt)(5)
那么,其二阶导数可以用式(6)表示:
s"(t)=-4π2aƒ2sin(2πƒt)(6)
将式(5)代人式(6),得到式(7):
s"(1)=-4π2ƒ2s(t)(7)
根据导数的定义,当t>△t且△t→0时,可得式(8):

2算法实现
2.1算法设计
卡尔曼滤波是用观测量(实际信号)对预测变量(模型信号)进行修正,滤波结果介于实际信号和模型信号之间。同样,滤波后的信号频率也介于实际信号频率和模型信号频率之间。为此,设计了一种基于涡街模型的卡尔曼滤波算法,以迭代的方法搜索涡街信号的频率。
首先,根据涡街信号的幅频关系设置初始系统模型频率。按照式(2)对液体介质管道上采集到的涡流信号的幅值和频率进行二次多项式拟合,得到在液体介质中50mm口径涡街流量计信号的幅值和频率的关系,如式(15)所示。
α=1.789x10-5ƒ2(15)
同理,对采集到的气体数据进行拟合,可以得到气体信号的幅值与频率的关系,如式(16)所示
α=2.622x10-8ƒ2(16)
用ƒm表示状态模型频率,用ƒmax,表示涡街信号的最大频率,令ƒm=ƒmax。这样设置的目的是减少迭代次数和计算量。于是,式(3)中的系数矩阵A可用式(17)表示。
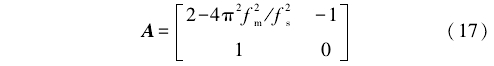
当流速低时,涡街信号能量弱,噪声较大,因而噪声系数D较大;反之,噪声系数D较小。由此可见,噪声系数D与涡流频率ƒ成反比。多次实验数据分析表明,当D为观测信号αmax与涡街信号模型幅值α之比时,得到了理想的良好滤波效果,如式(18)所示。
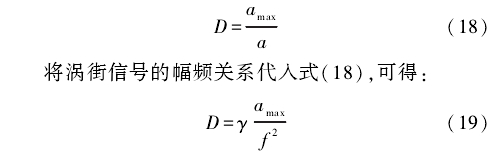
式中:ϒ为不同介质中幅频关系的系数。
以50mm.口径管道的液体介质为例,对不同流量点采集的实验数据进行噪声系数D和信号频率ƒ的曲线拟合,拟合得到的关系式如式(20)所示。


最后,对最优估计Xk的周期进行统计分析,去除组内杂散数据后,取平均值的倒数作为涡街信号的频率,以得到的频率为涡街信号的新系统模型频率,对原始信号进行卡尔曼滤波。由于原始信号中涡街信号的频率保持不变,滤波器输出频率介于涡街信号频率和模型频率之间,滤波器输出频率和模型频率在迭代中逐渐收敛到涡旋信号频率。当输出频率与模型频率的相对误差在预设值以内时,停止迭代,最终输出涡街频率。
2.2算法流程
具体的算法步骤整理如下。
步骤一:采集一组观测信号序列Yk(k=1,2,3,,,N),对卡尔曼滤波参数B、H、Q、D初始化,并拟合出R与ƒ的关系式。
步骤二:首先,根据在迭代中不断变化的状态模型频率ƒm.对转移矩阵A和观测噪声协方差R进行参数更新;然后,对观测信号Yj进行状态预测,并输出最优估计信号序列Xk(h=1,2,3,,N)。
步骤三:通过脉冲翻转整形方法对最优估计信号序列进行频率计算。设置翻转上阈值Athr和翻转下阈值-Ar,当信号由低向高上升到Athr时,将输出的信号电平置高。当信号由高向低下降到-Athr时,将输出的信号电平置低,最终输出脉冲信号序列Z(h=1,2,3,,N)。通过脉冲计数方法直接求出脉冲信号Zk的周期序列T;(i=1,2,3,.,M),计算出周期序列Ti,的平均值Tavg,得到滤波输出信号的平均频率ƒout=1/Tavg。
步骤四:输出信号频率ƒout和状态模型频率ƒm若满足Iƒout-ƒmI≤ƒmx1%,则跳转到步骤五。若lƒout-ƒm|>ƒmx1%,且ƒout≥ƒmin,则令fm=fe,并跳转到步骤二;否则,应停止搜索并保持输出上一轮信号处理得到的涡街信号频率,跳转到步骤一。
步骤五:输出信号幅值Aout和拟合的涡街信号幅值α的关系若满足|Aout-αl<αx10%,则判断为涡街信号频率输出频率ƒout,并跳转到步骤一;若|Aout-α|≥αX10%,则认为是周期振动噪声频率,跳转到步骤六。
步骤六:令ƒm=ƒmin9时,继续向下搜索涡街信号频率。当ƒm≥ƒmin时,跳转到步骤二。若输出频率ƒout,仍等于噪声频率,则重复步骤六;否则跳转到步骤四。当ƒm<ƒmin时,应停止搜索并输出上一次正确的涡街信号频率,并跳转到步骤一。
3实验验证
为验证本方法的有效性、测量精度和抗干扰性,采用仿真信号和实流信号在不同管径、不同介质下进行实验测试。
3.1仿真实验
本文带有管道噪声的涡街信号模型是基于牛津大学获得的涡街信号功率谱密度,Shao等在此基础.上加人时域波形规律和幅度衰减现象建立的涡街信号进行仿真模型分析。数学模型表达式如式(26)所示。
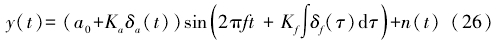
式中:α0为涡街信号幅值;f为涡街信号频率;Kƒ、Kα分别为调频灵敏度和调幅灵敏度,K,为涡街信号频率与采样频率的比值,设Kα=1;δα(t)和δƒ(t)分别为高斯白噪声和涡街信号幅度和频率的波动偏差;n(t)为其他噪声干扰,包括低频振荡干扰、工频干扰、周期振动干扰和随机干扰。
在上述模型中,加人具有多个单自由度阻尼弹性系统线性组合特性的瞬态冲击振动干扰模型,如式(27)所示。
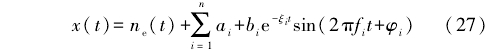
式中:n为系统的自由度,取n=6;ne(t)为高斯白噪声;ξi为阻尼系数;ƒi为振动频率;Φi为初始相位;αi、bi、ξi为常数,取值参考相关文献。
3.1.1本方法的仿真验证
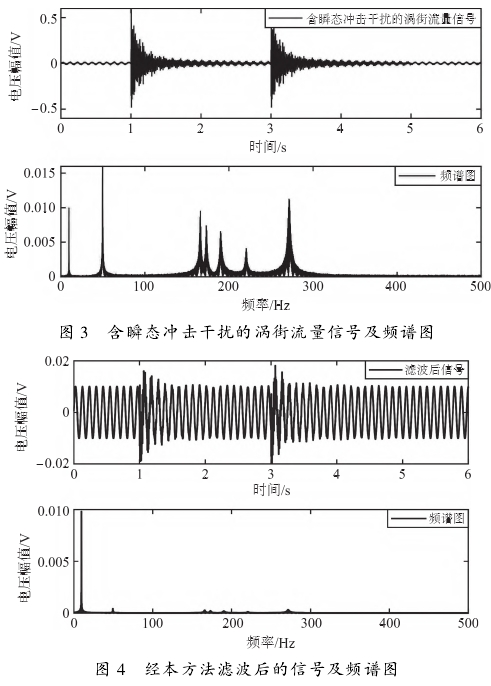
首先,验证本方法对瞬态冲击的滤波效果。涡街信号仿真模型的采样频率为10kHz、采样时间为6s,加入两次瞬态振动干扰,管道直径分别为25mm;和50mm,流体介质为气体和液体。以管径为25mm、频率为9.54Hz的液体介质信号为例,含有瞬态冲击干扰的涡街流量信号波形及其频谱图如图3所示经过本方法处理后的波形及频谱图如图4所示。从图3和图4中可以看出,瞬态冲击干扰被有效滤除了。
3.1.2本方法对比仿真实验
将本方法与传统卡尔曼滤波方法、经验模态分解方法(EMD方法)进行仿真实验对比,在液体介质中的仿真实验结果列于表1,在气体介质中的仿真实验结果列于表2。
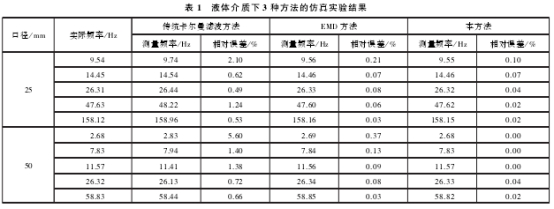

在表1、表2中,实际频率是指模拟涡街信号的频率,相对误差是指实测频率与实际频率的误差绝对值与实际频率的比值,按式(28)计算。从中可以看出,本方法的测量相对误差小于传统卡尔曼滤波方法和EMD方法的测量相对误差,在低流量的情况下,其测量低误差优势更为明显。
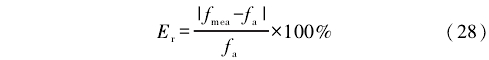
式中:Er为相对误差,ƒmea为实测频率,ƒa为实际频率。
3.2实流实验
本文采用由上海质量监督检验技术研究院提供的移动式气体流量标定装置进行气体介质下的仿真实验该装置由被检仪表、标准仪表、风机、工控机、稳压箱和变频器组成,其标定流量范围为0.5~270m3/h,测量相对扩展不确定度不大于0.63%,稳定性和重复性均不超过0.3%。
本文采用由上海质量监督检验技术研究院提供的移动式液体流量标定装置进行液体介质下的仿真实验。该装置由被检仪表、标准仪表、水泵、工控机、稳压罐和变频器组成。标定装置可提供近似稳定的流量,通过标定时间内的累计流量可验证装置的精度可达0.001m3/h。
实流实验的管道口径为50mm,流体介质为气体和液体,采样频率为10kHz,采样时间为6s。每组实验选取10个流量点,主要是受噪声影响较大的低流速信号。表3和表4分别为管径为50mm液体和50mm气体的3种方法的处理结果,其中实际频率为标定装置上标准表的信号频率。
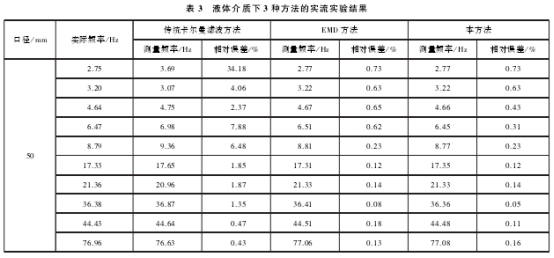
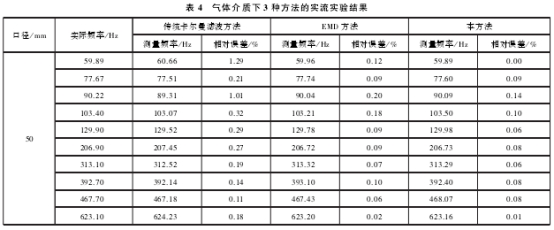
实流实验结果表明,相比于其他两种方法,本方法.具有更小的误差。
4结语
本文提出了一-种基于涡街信号模型的卡尔曼滤波的涡街流量计信号处理方法。首先分析了卡尔曼滤波算法的原理,利用微分原理和线性矩阵建立涡街信号的线性系统模型。模型的初始频率由涡街信号的最大频率决定,提高了算法的计算效率。而后结合模糊搜索和迭代算法对卡尔曼滤波算法进行改进,通过迭代搜索使滤波结果逐渐接近涡街信号。经验证,循环迭代次数一般在3~10次之间,复杂度低,响应速度快。接着为迭代循环设置终止条件,判断是否找到涡街信号,并通过涡街信号的特性设置边界条件,防止迭代过程发散。实现了卡尔曼滤波器的自适应滤波功能。最后通过仿真实验和实流实验计算信号频率和相对误差,并与传统的卡尔曼滤波方法和EMD方法进行比较。实验结果表明,与其他两种方法相比,所提方法具有测量精度、抗振性。涡街信号的幅值与频率的关系是本文算法初始参数和输出条件的设计依据,其系数易受流体温度和探头损耗的影响,从而影响算法精度。因此,本文设计的算法适用于低流体密度、低腐蚀、低温波动的场合。
本文来源于网络,如有侵权联系即删除!