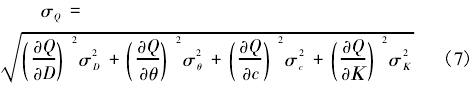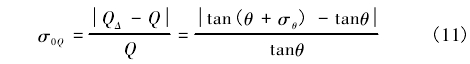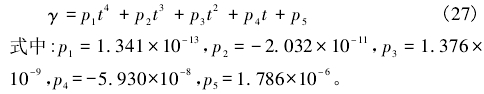摘要:流量测量是影响水轮机效率测试精度最主要的因素。大管径流量测量的方法主要采用超声波法,然而,其测量精度及误差构成尚无有效的校验方法。结合时差法超声波流量计的测流原理,推导得到流量综合误差,建立测流误差描述模型。提出一种基于流量测量理想系统来进行误差分析的量化方法,为超声波测流系统的误差分析与控制提供一种新的途径。通过测流.理想系统对超声波测流精度的影响因素进行仿真研究,分析了各项参数测量误差对系统综合误差的影响,针对影响较大的主导因素提出了相关修正方法,并对系统综合误差的控制进行了分析。最后搭建实验系统进行研究,实验结果初步验证了该方法的有效性。
0引言
水轮机效率是水电站经济运行的基础数据。国际电工委员会推荐的热力学法“在国内鲁布革电站进行过尝.试四,其实施难度较大。影响水轮机效率测试精度的主要因素是流量测量,特别是大管径流量测量。目前,大管径流量测量的方法主要是超声波法,测量原理应用最多的是时差法时差法测流原理简学直观,但要提高测流精度涉及因素较复杂7-四,而且实验所得数据本身就存在误差,测流误差的校验尚无简单有效的方法,因此研究相关因素的影响并有针对地进行优化和控制对提高测量精度十分必要。
目前,对测流精度影响因素已基本取得共识。超声波测:流误差的原因主要有3个方面:1)断面流速均匀计算造成的误差;2)超声波传感器安装和测量精度造成的误差(声音传播信号是否能被传感器正确收到,声路长度和声路角的测量误差);3)环境及介质对超声波流量计时间计算造成的误差。目前的研究基本.上都是围绕这3个方面展开的。分析了影响测量精度的因素,对温度、流速和管道内置反射片所造成的测量误差进行了分析,提出了具体的误差修正补偿方法,但其反射片安装在流体内部,对流场可能有影响且不便测量操作;杨志勇等中在推导流量计算公式的基础上得出影响测量结果的主要因素,有针对性的提出了延长声波法、温度补偿法、流量修正法、系统集成化设计,但其重点在信号处理上且针对小管径进行分析;杨声将等对噪声、脏污、压力及温度测量对超声波流量计计量系统性能的主要影响因素以及控制对策进行了分析探讨,但实验现场仍不能满足相关要求,造成仪器测量的不正确性;耿存杰等以主要介绍了利用实验室现有的液体流量标准装置,对超声波流量计在不同管道材质、不同管径的条件下进行流量系数的修正,但条件变化时需重新进行标定,不便于使用。
本文讨论了造成超声波流量计测流误差的影响因素,推导得到流量综合误差,提出一种基于流量测量理想系统进行误差分析的量化方法,分析了单个因素对流量相对误差的影响程度,针对主导因素给出了相应的修正方法,最后对综合误差的控制进行了分析,为流量的修正提出了新思路。
1时差法超声波流量计工作原理
超声波流量计测量系统最常用的测流原理是“时差法”。超声波换能器采用的是管外“Z"型安装方式,测量原理如图1所示。探头1发射信号,信号穿过管壁1、流体、管璧2后被另一侧的探头2接收到;在探头1发射信号的同时探头2也发出同样的信号,经过管壁2、流体、管壁1后被探头1接收到;由于流体流速的影响超声波在顺流和逆流情况下的传输时间t1和t2不同,因此根据时间差便可求得流速,进而得到流量值。
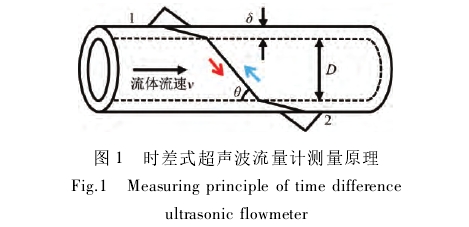
如图1所示,记管道内径为D.超声波在水中声速为c,超声波传播线路上的流体流速为v,声路角为θ,超声波在换能器和管壁中的总传播时间7τ0,则顺流、逆流传播时,超声波传输时间为:

时差式超声波流量计测量通常采用的是超声波传播路径上流体的线平均流速,而实际管道横截面上的流速分布是呈抛物线形态的,这就造成了断面流速计算造成的误差,具体如图2所示。

由图2可知,流体线平均流速0与截面平均流速VD存在以下关系:
大管径超声波流量计的现场校验试验比较困难,其流量测量本身就存在一-定误差,采用试验验证方法是没有意义的。本文提出一种基于理想系统的验证方法,即按超声波测流的布置形式.给出理想条件下的参数值,假设存在参数测量误差,按上述公式进行计算,得到各项参数对流量测量误差的影响程度.进而分析得到影响流量测量误差的主导因素,再进行误差修正。
设置一个理想系统:被测流体为清水,管道内径为D=3.00m,超声波流量计安装角为θ=40°,水体温度t=20℃,超声波传播速度为c=1485.00m/s,流体截面平均流速vD=4.00m/s.流量为Q=28.26m3/s。理想条件下时间测量仪器精度完全达到要求时得到的时间差为△t=1.30x10-5s。
2单因素误差分析
由式(6)知流量与管道内经D、声路角θ、超声波在水中的速度c、及流量系数K有关,因此流量测量中重点考虑这4项因素。
根据间接测量的误差理论,对式(6)做变换可得流量的绝对误差σQ,为:
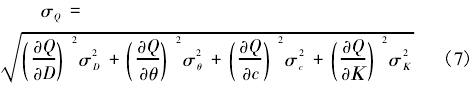
将式(6)代入式(7),可得:
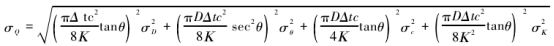
式中:σx表示变量{D,θ,c,K}的绝对误差。
在超声波流量计安装完成后,取理想条件所对应的各参数值为基值。将式(8)两边同时除以Q,化简整理后得相对误差为:

管径测量精度一般能达到0.1%,按相关倍数取值得到不同管径误差σ0D时的流量误差如表1所示。
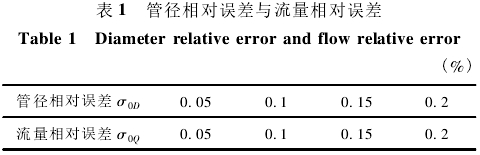
由式(10)可知,管径的相对误差会造成1倍的流量相对误差,由此可见理论.上管径误差对流量误差有着较大的影响。在实际工程应用中,大管径的测量误差较小,例如,管径为3.0m,测量误差为±0.05%时,误差绝对值为±1.5mm,而实际测量时,误差绝对值远小于±1.5mm。对照表1可知,管径测量误差造成的流量误差能控制在远小于±0.1%以内,并且钢管结垢现象也不太明显,因此管道测量精度的影响可以先忽略。
2.2声路角误差
由式(6)可知,当声路角测量存在误差σθ时,流量相对误差为:
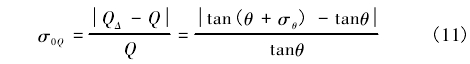
分别取不同声路角θ和声路角误差σθ,得到的流量相对误差如表2所示。
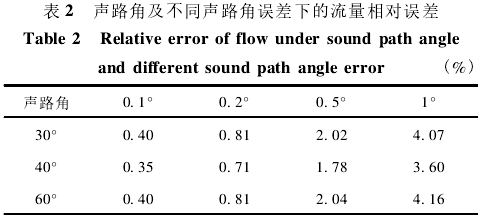
声路角为40°时,0.5°的声路角误差造成的流量相对误差能达到1.78%左右的,1°的误差造成的流量误差高达3.6%,随着声路角误差的增大流量相对误差增长也较为明显。同--声路角误差下θ=30°和θ=60°时的流量相对误差相近,与两者相比θ=40°时的误差较小,因此,初步推断存在一个最佳声路角使得流量相对误差最小。
2.3声速误差
声速会随温度变化而变化,根据威拉德研究给出的水声速与温度关系式”得到标准大气压下水中声速与温度的关系式可写为:

在20℃时超声波传播速度为c=1485m/s.当水温发生变化,t=0℃时,c=1422.838m/s,t=40℃时,c=1528.678m/s,对应的流量相对误差分别为8.266%、5.889%。
如若忽略温度的变化,由上两式知20C的变化量下流量相对误差平均能达到7%左右。并且根据该方式计算得到在0~40℃范围内超声波传播速度差值可达105.84m/s,对应流量测量误差为14.155%。因此根据相关关系式来进行声速调控很有必要。
在该理想系统“下,取不同声速误差,代入式(13)可得流量相对误差如表3所示。
由表3可知.1%的声速误差会造成2%的流量误差,但同一时段的温度变化并不明显,其误差很小可以控制在0.01%范围内,其波动可以通过与敏感的温度传感器相结合的方法将温度变化引起的声速改变及时传递给流量计,以此来减小误差。

2.4流量系数K造成的误差
流场流态对流量测量有一定的影响,其影响主要是通过其流速系数K来体现。
管道内的流体实际流速分布规律为:

由上述分析知,修正系数K与雷诺数Re的大小有着直接关系,并且其变化范围较广取值很难确定,因此根据外界因素不同得出两者关系对流量的正确测量有很重要的影响。
综上所述,对流量测量影响较大的因素为声路角θ和修正系数K。
3主导因素修正
3.1声路角误差修正
由于直接测量角度较为困难,且其测量仪器精度不能达到要求,因此考虑在测量方式上进行优化,提出一种依据长度安装要求达到控制声路角的方法。

图4所示为流量相对误差与声路角的关系。由图4可知,在声路角测量误差较小时,流量测量相对误差随声路角(安装角)大小的变化不明显,如图中红线(σθ=0.1%)所示。反之,若声路角测量误差较大,则流量相对误差随声路角的变化呈抛物线变化,如图中绿线(σθ=1°)所示,且存在一个最小值。声路角不变时,流量相对误差会随着绝对误差的增大而增大。
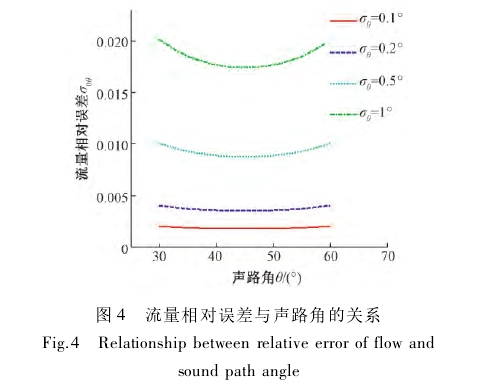
令შσ/შθ=0,有θ=45°时,流量的相对误差σ0Q取最小。
3.2K值的修正
K系数与流体型态有关且随雷诺数变化而变化,研究不同型态下的K系数随雷诺数变化规律有利于流量补偿计算和提高测量精度。
由式(24)可知,层流时的修正系数K=4/3,但对大管径来说,场内流态一般是紊流情况。因此,本文重点分析紊流时的流量系数K的修正。
紊流时修正系数与雷诺数有关,经验公式为:
K=1.119-0.011xlgRe(25)
依据式(25)可知.流量系数与雷诺数呈线性关系,雷诺数变化直接影响流量系数的取值。本文考虑根据雷诺数相关的变量来对K值进行修正。雷诺数计算公式为:

式中:V为平均流速;D为管道内经;Ƴ为流体运动粘度。
由式(26)可知,雷诺数大小与3个变量有关。当管径一定时,雷诺数会随着平均流速和流体粘度变化而变化。水的粘度随温度的变化而变化,温度变化会影响到雷诺数,进而影响流量修正系数K的值。因此找出粘度随温度的变化关系对K的正确性有着一定的影响。
流体粘度受流体温度的影响具有非线性特点,通过拟合温度与运动粘度值,得到不同温度下水的运动粘度的曲线,如图5所示。
多项式拟合表达式为:
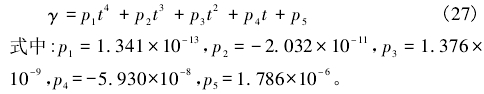
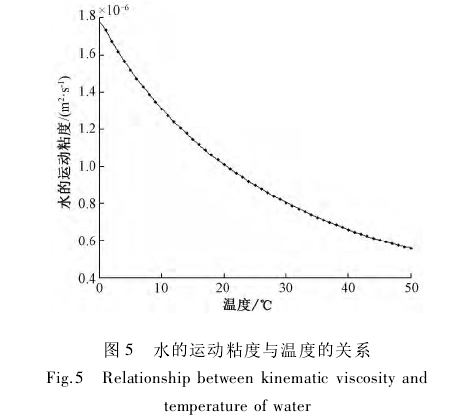
随着温度的升高,水的粘度非线性特征愈发明显。在0~50℃范围内水的粘度值差值可达到1.2x10-6m2/s,对应的雷诺数误差为66.67%,不容忽视。
将得到的拟合曲线依次代入式(19)、(20)得:
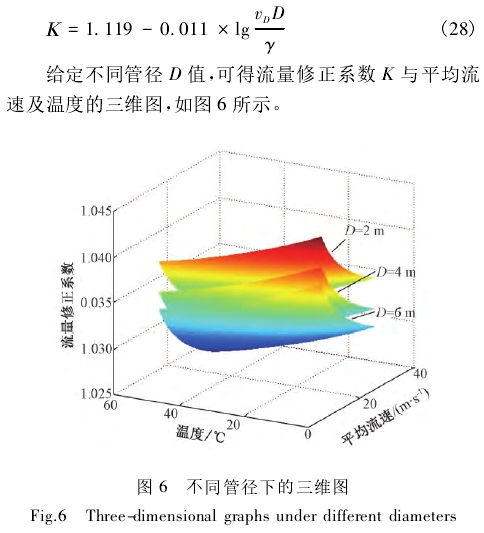
由图6可以看出,同一管径条件下,流量系数随平均流速和温度的增加都呈非线性减小趋势。其他条件一定时,随着管径D的增大流量系数K值会减小。
此修正方法将温度和流速变化与K值联系起来,两者任一值发生变化都能找到相对应的修正系数值,为准.确测得流量提供了一定的理论基础。
4系统误差控制
根据式(9)知流量相对误差由内径D、声路角0、声速c及流量系数K值组成,因此系统的误差控制需要对这4个因素进行综合考虑。
若原设理想系统中的流量测量误差精度要控制在±0.5%以内,即σoQ<0.5%。由综合误差式(9)知,各因素至少要满足σ0x<0.5%。
1)内径误差
目前的一-些管径测量仪器已经能达到较高的精度,像激光扫描测径仪精度最高可达0.5μm,其误差可控制在0.005%以内甚至更小,完全满足单因素精度要求。由于管径在制造过程中可能存在一定的误差,因此在对管径进行测量时可在安装位置处采用多处多次测量求平均值的方法来尽可能减小此部分误差。
2)声路角误差
声路角测量较难进行,将角度测量转化成距离测量后,在安装时按照需要角度进行计算后再安装便能减小其误差,其误差可以控制在0.05%以内,也满足单因素的误差要求。.
3)声速误差
同一时段内的温度变化很小,因此其造成的声速变化不明显,根据.上述声速温度修正公式进行修正后,其误差便可控制在0.1%以内,满足单因素的精度要求。
由于管径测量精度很高,在此忽略此项误差。将θ=45°,σ0θ=0.05%,σ0C=0.1%代入式(9)得:
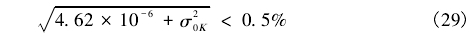
由上式得至少要满足σ0K<0.45%系统才能达到要求。若想进一步减小综合误差,则需优化各因素测量仪器,使其误差控制在更小范围内。
根据上述分析,超声波测流精度控制中,最困难的因素就是管道流速形态的处理,即本文中提到的系数K。如何进--步提高管道流速分布对测量的影响及得到其修正方法,尚需开展进一步研究。
5实验系统搭建
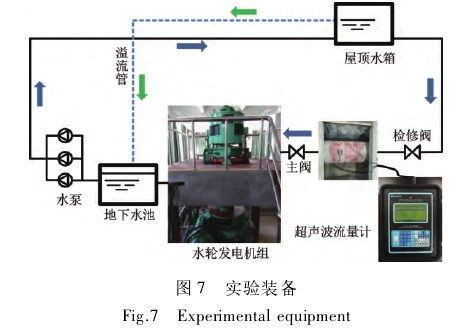
对于大管径超声波流量计测流的验证性实验是比较困难的。利用水机电耦合真机实验室,在引水管直管段上搭建实验平台来进行了相关实验,对本文提出的影响测量精度几方面的因素进行了试验分析。
试验条件:安装点选取位置前后直管段距离均满足安装要求,直管段外径D=616mm,管壁厚度δ=8mm.实验环境温度15℃,流量测量仪器采用的是康创TY1010PW单声道便携式超声波流量计,其精度为1%。实验装备如图7所示。
通过效率试验测得相关数据,在实验中改变出力P来测流量Q,并根据上述分析得到了流量系数K值,数据如表5所示,水轮机功率与流量的关系如图8所示。
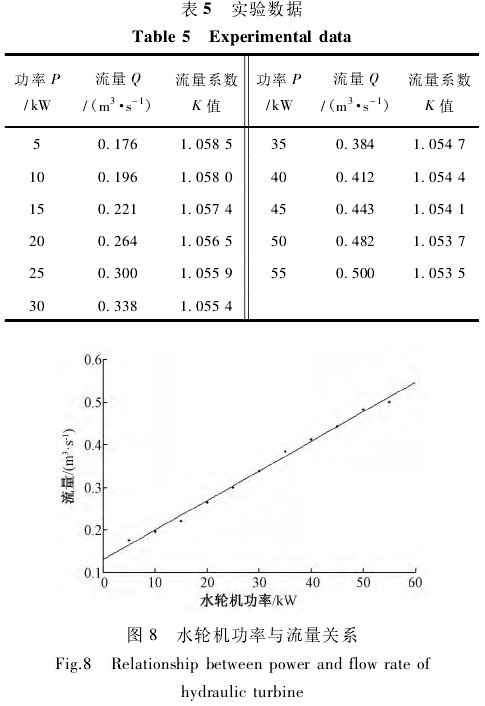
由图8可以看出,水轮机功率与流量的关系与厂家给出的流量特性是一致的。本实验各项误差控为σD=0.005%,σθ=0.05%,σc=0.1%。从综合误差分析来看,当流量系数K值满足σoK<0.45%时系统误差便可控制在0.5%以内。
由表5可以看出。流量变化从0.176~0.5m/s时,流量系数K值从1.0585~1.0535,变化范围较小。取功率P=55kW时.测得的流量Q=0.5m3/s,考虑其精度1%,则实际流量范围为0.495~0.505m3/s,从表可以看出,流量系数K值的变化波动值约为0.0005,精度可达到0.05%,其误差范围完全满足综合误差控制要求,因此,初步推断该方法有效。
6结论
本文提出了一种基于理想测流系统的超声波流量计误差分析方法,讨论了造成超声波流量计测流误差的原因、误差产生影响因素。通过量化方法对各影响因素进行讨论,针对主导因素给出了相关的误差修正方法,对综合误差控制进行分析并开展了试验进行验证。从实验结果可初步推断该方法是有效的。基于理想测流系统分析方法弄清了各参数的影响程度,对于现场安装和进行实测试验都有一定的指导作用,为后期超声波流量计的误差修正提供了新思路。该方法在优化水轮机效率计算精度的同时也为超声波流量计的设计提供了参考。
本文来源于网络,如有侵权联系即删除!