宫交H打桩HH灌尿,欧美性生交XXXXX久久久,АⅤ资源天堂资源库在线,国产激情一区二区三区

1.脉动流特性
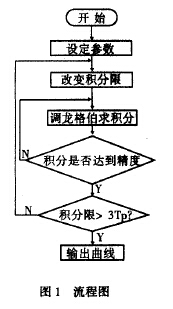
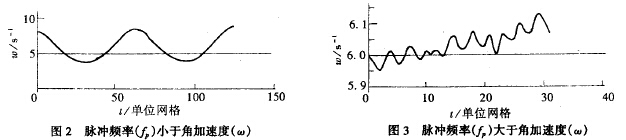
    几乎所有的管道流都是不稳定的，不论是层流状态还是湍流状态下都存在各种干扰。所谓脉动流是指流体在测量区域的流速是时间的函数，但在一个足够长的时间段内有一个恒定的平均值，这个值决定于脉动流的流动规律。
    真正的管道定常流仅出现在层流中，大多数工业管流均出现湍流现象，试试一种统计意义上的定常流，脉动流会影响涡轮流量计的测量精度，有时会使其测量值严重失真，所以工业上迫切需要研究脉动流对其测量精度的影响。
    脉动无处无时不在，但测量却非常困难，我们通常只能测量出脉动的主要参数，如辐值、频率和波形，然后通过这些参数分析脉动可能给流量计造成的影响。
2.脉动流对涡轮流量计测量精度的影响
2.1特性方程及计算
    涡轮流量计以动量矩守恒定理为基础的一种速度式流量仪表，对非稳定流由于转子叶片和相关传动装置的共振、转子的转动惯量、脉动的形状、转子和齿轮摩擦阻力及转子瞬时转矩等因素影响，使涡轮流量计产生很大的误差，用机翼理论来分析作用在转子上的驱动力矩和阻力矩，可得到其运动方程:

    式中J为叶片转动惯量，θ为叶与轴线之间的夹角，r为涡轮叶片的平均半径，A为管道流量面积，ρ为流体密度，ω为涡轮的旋转角加速度，Q为通过管道流量。
    若把脉动流表示为Q=asin2πfpt，经过分析整理，可得出涡轮旋转角加速度与脉动流各参数的关系：22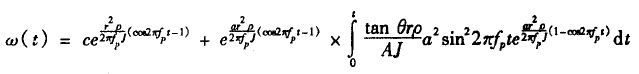

其中C为稳态时的ω值。
    对特定的涡轮流量计和不同的脉动流，可编程计算出（2）式在脉动周围内各离散点所对应的ω（t），据此计算可画出ω（t）曲线，其流程图如图1：
2.2结构与分析
    经过计算分析，发现导致流量计产生误差的主要因素是脉动流的频率，所加的正弦脉动流的频率与稳态下涡轮的旋转角加速度的关系为ω=2πfp(1/qm)r2时，相应曲线与输入正弦曲线最为接近，与理论分析基本吻合，多次改变脉动流频率、振幅参数，发现有时图形失真非常厉害，通过对多幅图形的比较，发现有如下规律：（见图2、3）

当脉动流频率fp大于旋转角加速度ω时，仪表的相应曲线开始失真，脉动频率导致相应曲线的幅值发生改变，经过分析发现，脉动频率越大，响应幅值越小，脉动频率越小，响应幅值越大，即随着频率的增大，响应失真程度随着增大，但最终有趋于稳定的趋势。 当脉动流频率fp大于旋转角加速度ω时，响应曲线的失真程度随脉动振幅的增大而加剧，但当脉动振幅小于某一振幅值时，其变化可认为不影响涡轮流量计的精度；当脉动频率fp小于旋转角加速度ω时，响应曲线的失真程度与脉动振幅的变化无关联。 对于形状不失真的响应曲线，其响应曲线的幅值还与其它参数有关。经研究发现，对测量误差影响较大的参数还有叶片转动惯量J和叶片的初始旋转角加速度C.J越小，响应曲线的幅值越大，J越大，响应曲线的幅值越小，但J太大或太小都会影响响应曲线的幅值失真过大，其值取在2*10-6-3*10-6（kg.m2）之间时，响应曲线最好，从参数分析可知，响应曲线与输入脉动曲线之间有一个位移，此位移的大小主要是与初始值C有关。

3.结论
   从以上分析计算可知，脉动流频率对涡轮流量计的测量精度影响最大，当脉动频率fp小于旋转角加速度ω时，流量仪表的响应曲线与输入脉动曲线相似，测量结构接近于真值；脉动振幅对涡轮流量计的测量精度存在影响，但当脉动振幅小于某一振幅值时，可认为其不影响涡轮流量计的精度；叶片转动惯量J和叶片的初始旋转加速度C也对涡轮流量计测量精度有影响。

本文智能涡街流量计来源于网络,如有侵权联系删除转载请注明出处！！！